A Formal Methods Approach to Pattern Synthesis in Reaction Diffusion Systems
Paper and Code
Sep 12, 2014
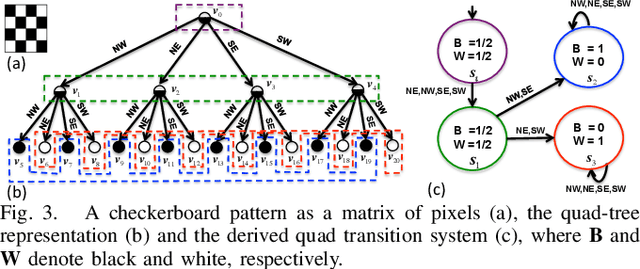

We propose a technique to detect and generate patterns in a network of locally interacting dynamical systems. Central to our approach is a novel spatial superposition logic, whose semantics is defined over the quad-tree of a partitioned image. We show that formulas in this logic can be efficiently learned from positive and negative examples of several types of patterns. We also demonstrate that pattern detection, which is implemented as a model checking algorithm, performs very well for test data sets different from the learning sets. We define a quantitative semantics for the logic and integrate the model checking algorithm with particle swarm optimization in a computational framework for synthesis of parameters leading to desired patterns in reaction-diffusion systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge