A Fast Sampling Gradient Tree Boosting Framework
Paper and Code
Nov 20, 2019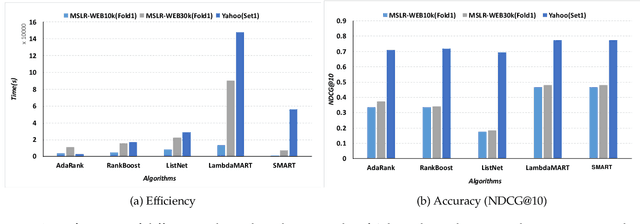
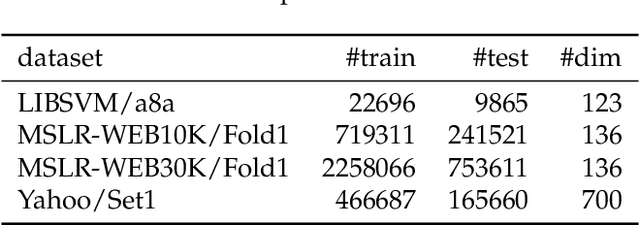
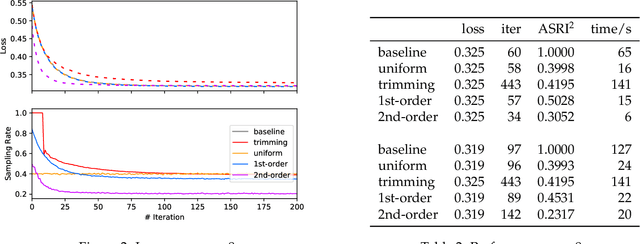
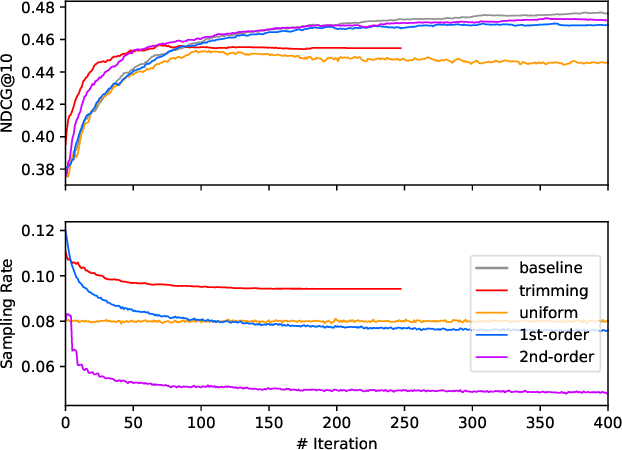
As an adaptive, interpretable, robust, and accurate meta-algorithm for arbitrary differentiable loss functions, gradient tree boosting is one of the most popular machine learning techniques, though the computational expensiveness severely limits its usage. Stochastic gradient boosting could be adopted to accelerates gradient boosting by uniformly sampling training instances, but its estimator could introduce a high variance. This situation arises motivation for us to optimize gradient tree boosting. We combine gradient tree boosting with importance sampling, which achieves better performance by reducing the stochastic variance. Furthermore, we use a regularizer to improve the diagonal approximation in the Newton step of gradient boosting. The theoretical analysis supports that our strategies achieve a linear convergence rate on logistic loss. Empirical results show that our algorithm achieves a 2.5x--18x acceleration on two different gradient boosting algorithms (LogitBoost and LambdaMART) without appreciable performance loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge