A Fast PC Algorithm with Reversed-order Pruning and A Parallelization Strategy
Paper and Code
Sep 10, 2021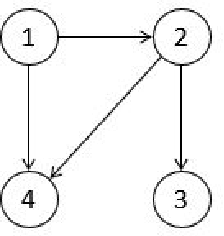
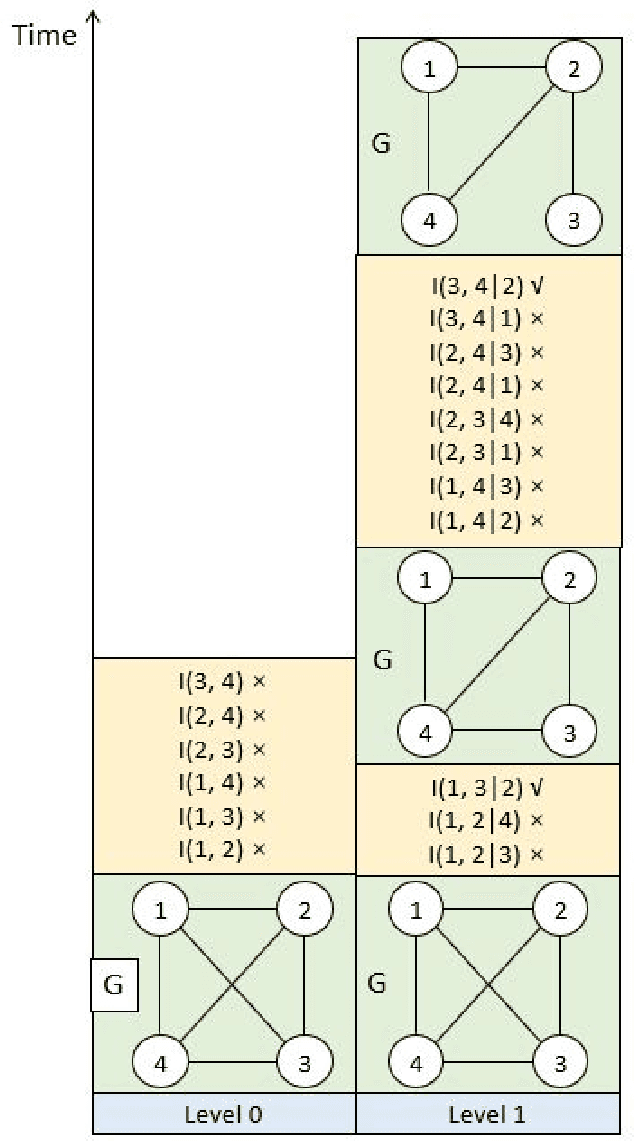
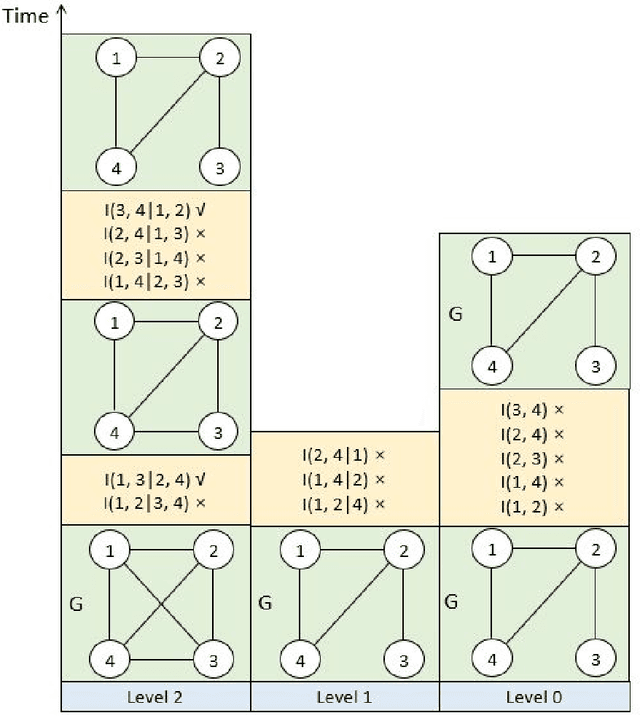
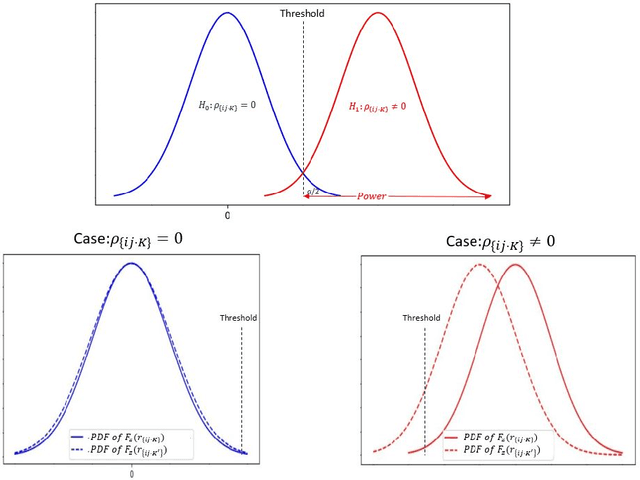
The PC algorithm is the state-of-the-art algorithm for causal structure discovery on observational data. It can be computationally expensive in the worst case due to the conditional independence tests are performed in an exhaustive-searching manner. This makes the algorithm computationally intractable when the task contains several hundred or thousand nodes, particularly when the true underlying causal graph is dense. We propose a critical observation that the conditional set rendering two nodes independent is non-unique, and including certain redundant nodes do not sacrifice result accuracy. Based on this finding, the innovations of our work are two-folds. First, we innovate on a reserve order linkage pruning PC algorithm which significantly increases the algorithm's efficiency. Second, we propose a parallel computing strategy for statistical independence tests by leveraging tensor computation, which brings further speedup. We also prove the proposed algorithm does not induce statistical power loss under mild graph and data dimensionality assumptions. Experimental results show that the single-threaded version of the proposed algorithm can achieve a 6-fold speedup compared to the PC algorithm on a dense 95-node graph, and the parallel version can make a 825-fold speed-up. We also provide proof that the proposed algorithm is consistent under the same set of conditions with conventional PC algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge