A Factorial Mixture Prior for Compositional Deep Generative Models
Paper and Code
Dec 18, 2018

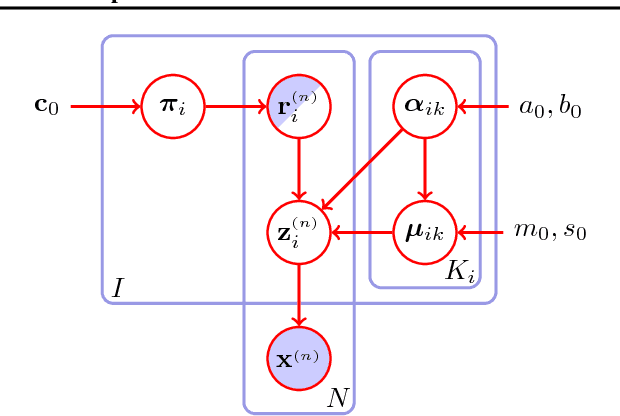
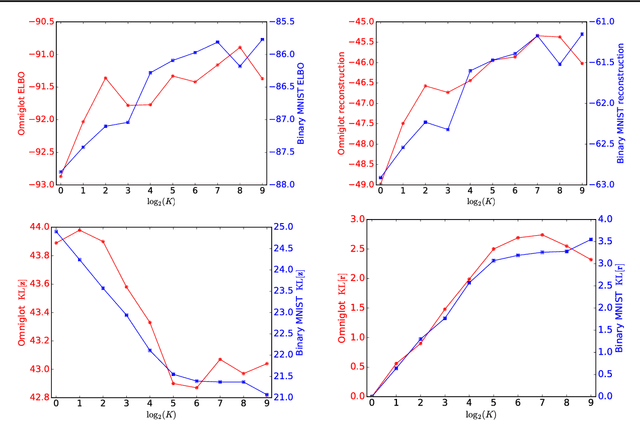
We assume that a high-dimensional datum, like an image, is a compositional expression of a set of properties, with a complicated non-linear relationship between the datum and its properties. This paper proposes a factorial mixture prior for capturing latent properties, thereby adding structured compositionality to deep generative models. The prior treats a latent vector as belonging to Cartesian product of subspaces, each of which is quantized separately with a Gaussian mixture model. Some mixture components can be set to represent properties as observed random variables whenever labeled properties are present. Through a combination of stochastic variational inference and gradient descent, a method for learning how to infer discrete properties in an unsupervised or semi-supervised way is outlined and empirically evaluated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge