A Distributed Hierarchical SGD Algorithm with Sparse Global Reduction

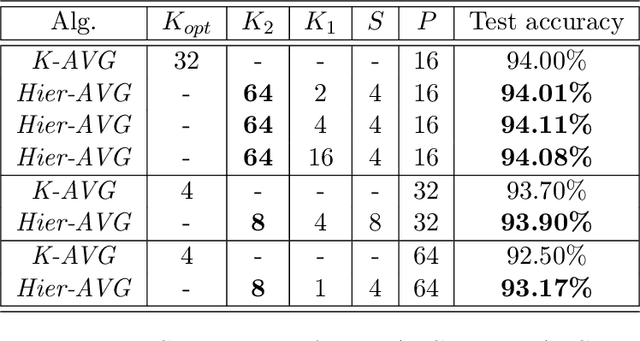
Reducing communication overhead is a big challenge for large-scale distributed training. To address this issue, we present a hierarchical averaging stochastic gradient descent (Hier-AVG) algorithm that reduces global reductions (averaging) by employing less costly local reductions. As a very general type of parallel SGD, Hier-AVG can reproduce several commonly adopted synchronous parallel SGD variants by adjusting its parameters. We establish standard convergence results of Hier-AVG for non-convex smooth optimization problems. Under the non-asymptotic scenario, we show that Hier-AVG with less frequent global averaging can sometimes have faster training speed. In addition, we show that more frequent local averaging with more participants involved can lead to faster training convergence. By comparing Hier-AVG with another distributed training algorithm K-AVG, we show that through deploying local averaging with less global averaging Hier-AVG can still achieve comparable training speed while constantly get better test accuracy. As a result, local averaging can serve as an alternative remedy to effectively reduce communication overhead when the number of learners is large. We test Hier-AVG with several state-of-the-art deep neural nets on CIFAR-10 to validate our analysis. Further experiments to compare Hier-AVG with K-AVG on ImageNet-1K also show Hier-AVG's superiority over K-AVG.