A Differential Geometric View and Explainability of GNN on Evolving Graphs
Paper and Code
Mar 11, 2024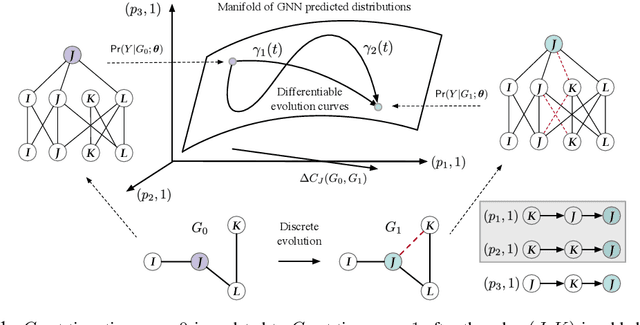
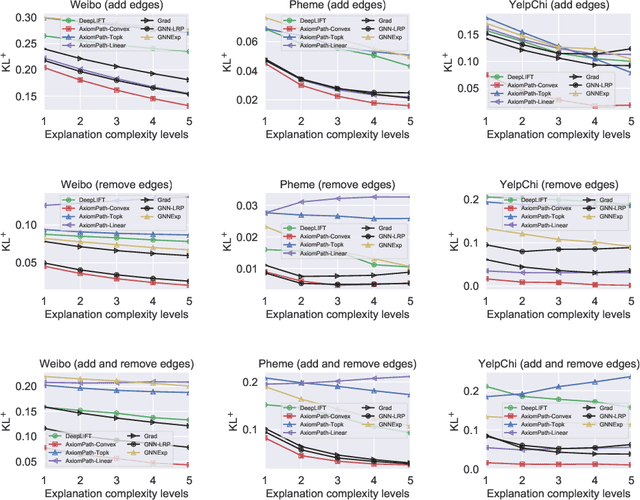

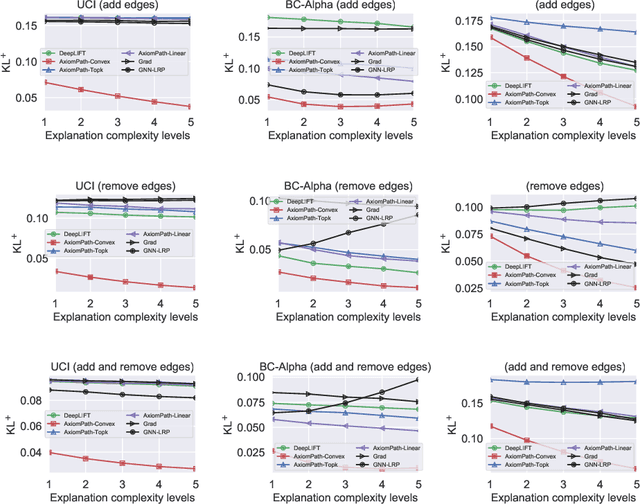
Graphs are ubiquitous in social networks and biochemistry, where Graph Neural Networks (GNN) are the state-of-the-art models for prediction. Graphs can be evolving and it is vital to formally model and understand how a trained GNN responds to graph evolution. We propose a smooth parameterization of the GNN predicted distributions using axiomatic attribution, where the distributions are on a low-dimensional manifold within a high-dimensional embedding space. We exploit the differential geometric viewpoint to model distributional evolution as smooth curves on the manifold. We reparameterize families of curves on the manifold and design a convex optimization problem to find a unique curve that concisely approximates the distributional evolution for human interpretation. Extensive experiments on node classification, link prediction, and graph classification tasks with evolving graphs demonstrate the better sparsity, faithfulness, and intuitiveness of the proposed method over the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge