A Decoupled and Linear Framework for Global Outlier Rejection over Planar Pose Graph
Paper and Code
Sep 18, 2022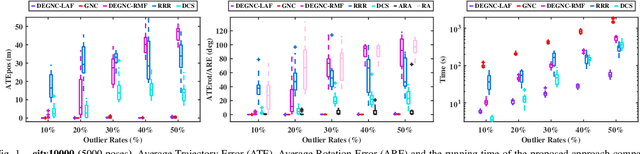
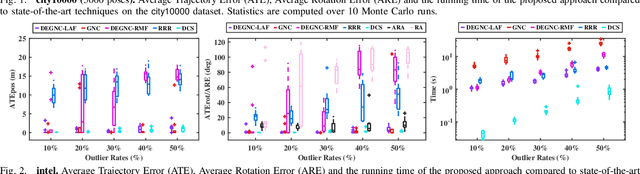
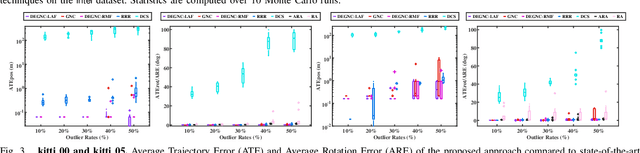
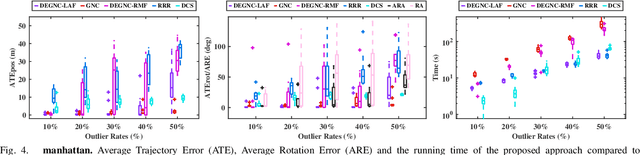
We propose a robust framework for the planar pose graph optimization contaminated by loop closure outliers. Our framework rejects outliers by first decoupling the robust PGO problem wrapped by a Truncated Least Squares kernel into two subproblems. Then, the framework introduces a linear angle representation to rewrite the first subproblem that is originally formulated with rotation matrices. The framework is configured with the Graduated Non-Convexity (GNC) algorithm to solve the two non-convex subproblems in succession without initial guesses. Thanks to the linearity properties of both the subproblems, our framework requires only linear solvers to optimally solve the optimization problems encountered in GNC. We extensively validate the proposed framework, named DEGNC-LAF (DEcoupled Graduated Non-Convexity with Linear Angle Formulation) in planar PGO benchmarks. It turns out that it runs significantly (sometimes up to over 30 times) faster than the standard and general-purpose GNC while resulting in high-quality estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge