A Convergence Theory for Over-parameterized Variational Quantum Eigensolvers
Paper and Code
May 25, 2022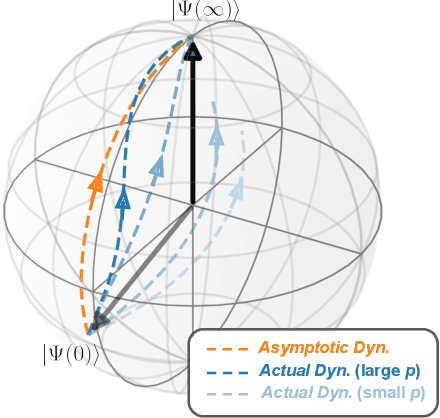
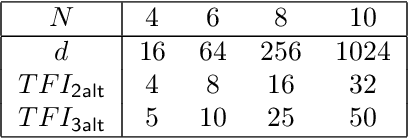
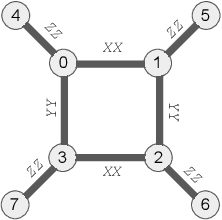

The Variational Quantum Eigensolver (VQE) is a promising candidate for quantum applications on near-term Noisy Intermediate-Scale Quantum (NISQ) computers. Despite a lot of empirical studies and recent progress in theoretical understanding of VQE's optimization landscape, the convergence for optimizing VQE is far less understood. We provide the first rigorous analysis of the convergence of VQEs in the over-parameterization regime. By connecting the training dynamics with the Riemannian Gradient Flow on the unit-sphere, we establish a threshold on the sufficient number of parameters for efficient convergence, which depends polynomially on the system dimension and the spectral ratio, a property of the problem Hamiltonian, and could be resilient to gradient noise to some extent. We further illustrate that this overparameterization threshold could be vastly reduced for specific VQE instances by establishing an ansatz-dependent threshold paralleling our main result. We showcase that our ansatz-dependent threshold could serve as a proxy of the trainability of different VQE ansatzes without performing empirical experiments, which hence leads to a principled way of evaluating ansatz design. Finally, we conclude with a comprehensive empirical study that supports our theoretical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge