A Computational Framework of Cortical Microcircuits Approximates Sign-concordant Random Backpropagation
Paper and Code
May 19, 2022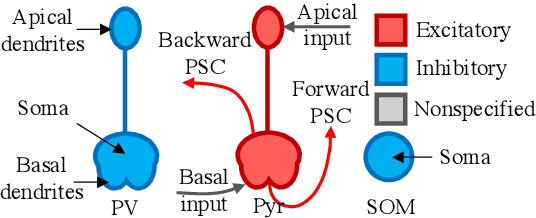
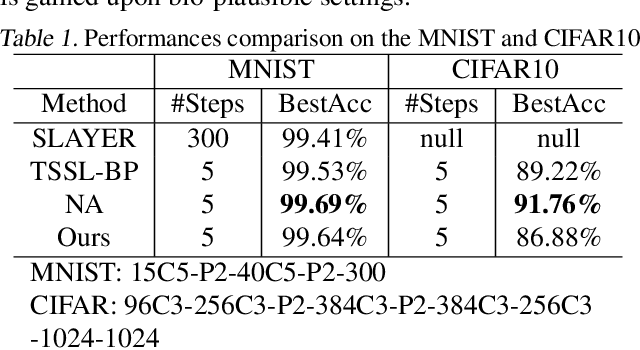
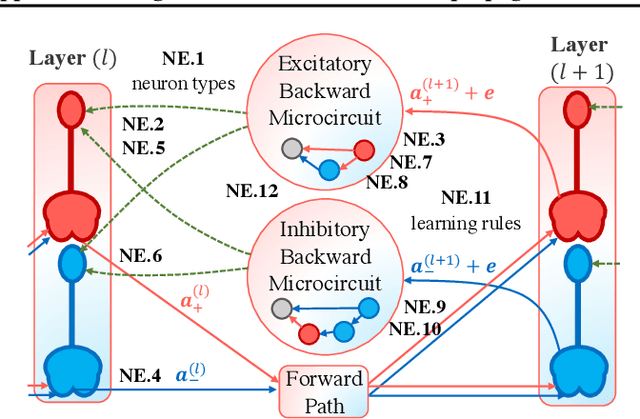
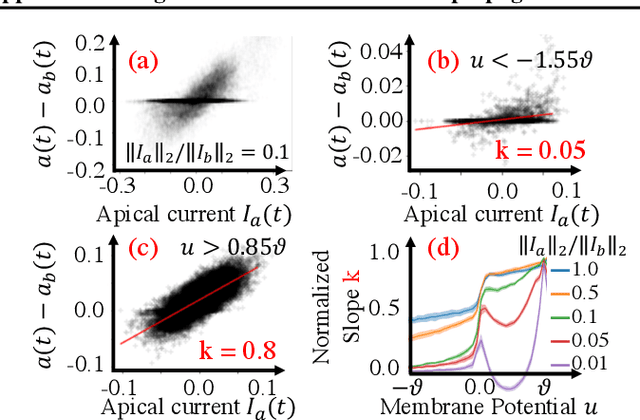
Several recent studies attempt to address the biological implausibility of the well-known backpropagation (BP) method. While promising methods such as feedback alignment, direct feedback alignment, and their variants like sign-concordant feedback alignment tackle BP's weight transport problem, their validity remains controversial owing to a set of other unsolved issues. In this work, we answer the question of whether it is possible to realize random backpropagation solely based on mechanisms observed in neuroscience. We propose a hypothetical framework consisting of a new microcircuit architecture and its supporting Hebbian learning rules. Comprising three types of cells and two types of synaptic connectivity, the proposed microcircuit architecture computes and propagates error signals through local feedback connections and supports the training of multi-layered spiking neural networks with a globally defined spiking error function. We employ the Hebbian rule operating in local compartments to update synaptic weights and achieve supervised learning in a biologically plausible manner. Finally, we interpret the proposed framework from an optimization point of view and show its equivalence to sign-concordant feedback alignment. The proposed framework is benchmarked on several datasets including MNIST and CIFAR10, demonstrating promising BP-comparable accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge