A Complete Derivation Of The Association Log-Likelihood Distance For Multi-Object Tracking
Paper and Code
Sep 08, 2015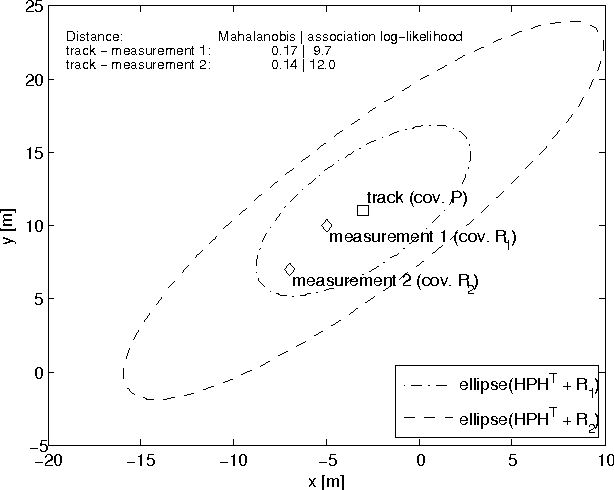
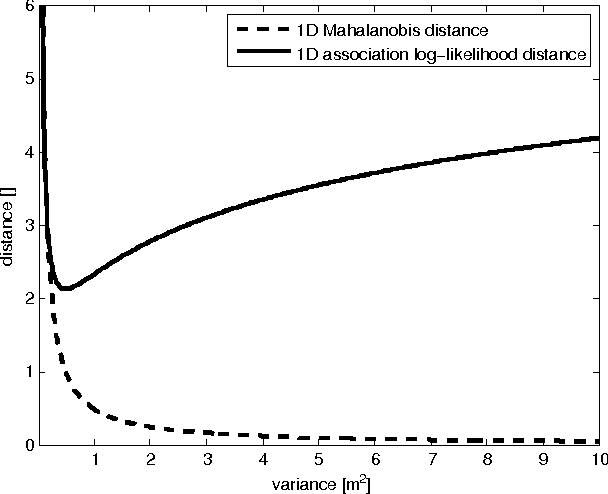
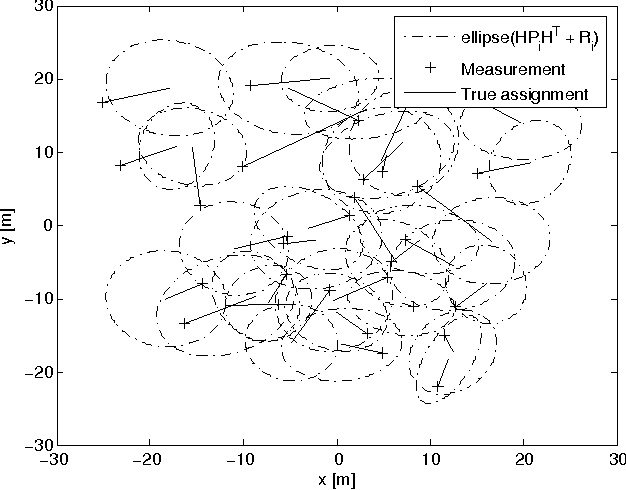
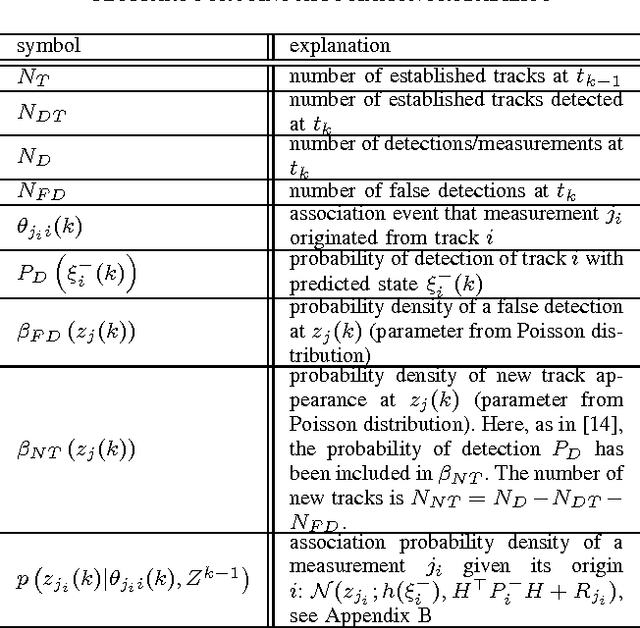
The Mahalanobis distance is commonly used in multi-object trackers for measurement-to-track association. Starting with the original definition of the Mahalanobis distance we review its use in association. Given that there is no principle in multi-object tracking that sets the Mahalanobis distance apart as a distinguished statistical distance we revisit the global association hypotheses of multiple hypothesis tracking as the most general association setting. Those association hypotheses induce a distance-like quantity for assignment which we refer to as association log-likelihood distance. We compare the ability of the Mahalanobis distance to the association log-likelihood distance to yield correct association relations in Monte-Carlo simulations. It turns out that on average the distance based on association log-likelihood performs better than the Mahalanobis distance, confirming that the maximization of global association hypotheses is a more fundamental approach to association than the minimization of a certain statistical distance measure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge