A Change-Detection based Framework for Piecewise-stationary Multi-Armed Bandit Problem
Paper and Code
Nov 20, 2017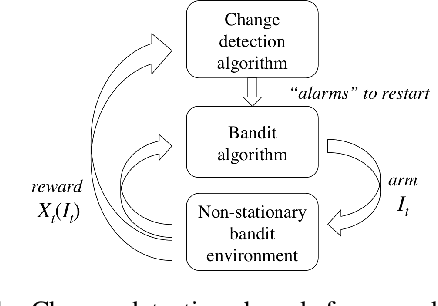

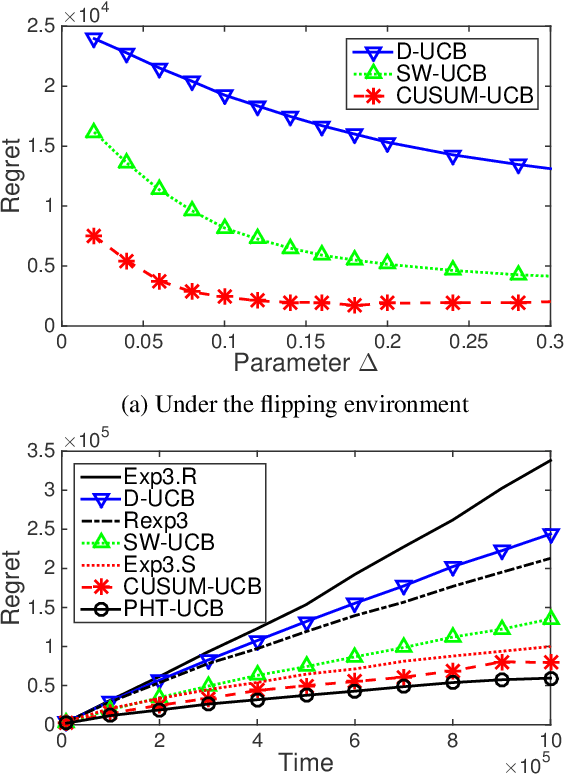
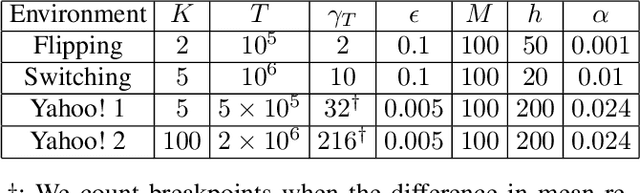
The multi-armed bandit problem has been extensively studied under the stationary assumption. However in reality, this assumption often does not hold because the distributions of rewards themselves may change over time. In this paper, we propose a change-detection (CD) based framework for multi-armed bandit problems under the piecewise-stationary setting, and study a class of change-detection based UCB (Upper Confidence Bound) policies, CD-UCB, that actively detects change points and restarts the UCB indices. We then develop CUSUM-UCB and PHT-UCB, that belong to the CD-UCB class and use cumulative sum (CUSUM) and Page-Hinkley Test (PHT) to detect changes. We show that CUSUM-UCB obtains the best known regret upper bound under mild assumptions. We also demonstrate the regret reduction of the CD-UCB policies over arbitrary Bernoulli rewards and Yahoo! datasets of webpage click-through rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge