A Block-wise, Asynchronous and Distributed ADMM Algorithm for General Form Consensus Optimization
Paper and Code
Feb 24, 2018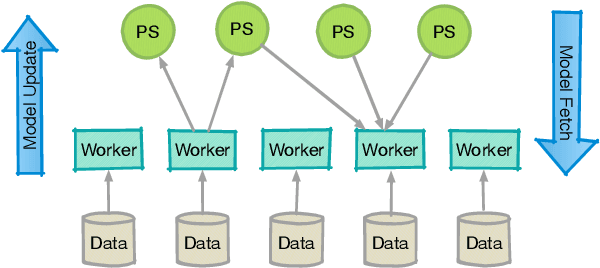
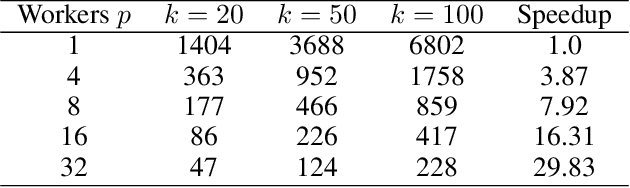
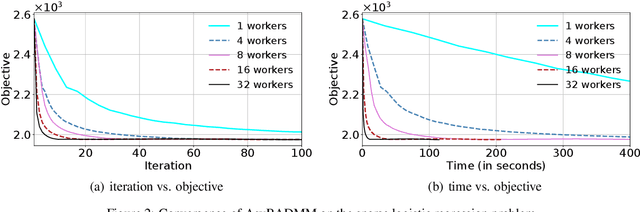
Many machine learning models, including those with non-smooth regularizers, can be formulated as consensus optimization problems, which can be solved by the alternating direction method of multipliers (ADMM). Many recent efforts have been made to develop asynchronous distributed ADMM to handle large amounts of training data. However, all existing asynchronous distributed ADMM methods are based on full model updates and require locking all global model parameters to handle concurrency, which essentially serializes the updates from different workers. In this paper, we present a novel block-wise, asynchronous and distributed ADMM algorithm, which allows different blocks of model parameters to be updated in parallel. The lock-free block-wise algorithm may greatly speedup sparse optimization problems, a common scenario in reality, in which most model updates only modify a subset of all decision variables. We theoretically prove the convergence of our proposed algorithm to stationary points for non-convex general form consensus problems with possibly non-smooth regularizers. We implement the proposed ADMM algorithm on the Parameter Server framework and demonstrate its convergence and near-linear speedup performance as the number of workers increases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge