A Bayesian Network Scoring Metric That Is Based On Globally Uniform Parameter Priors

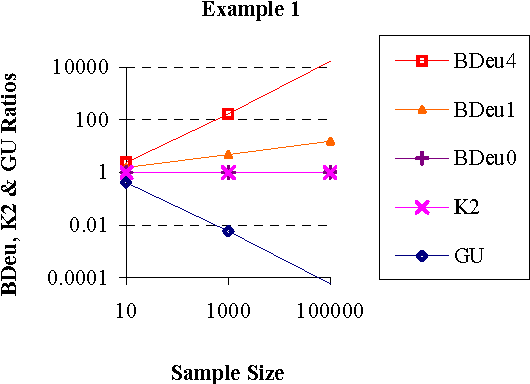
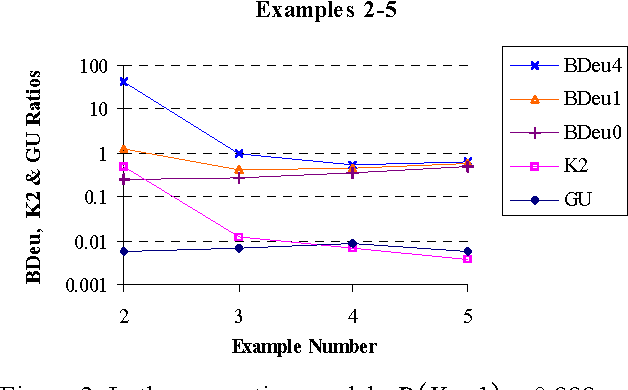
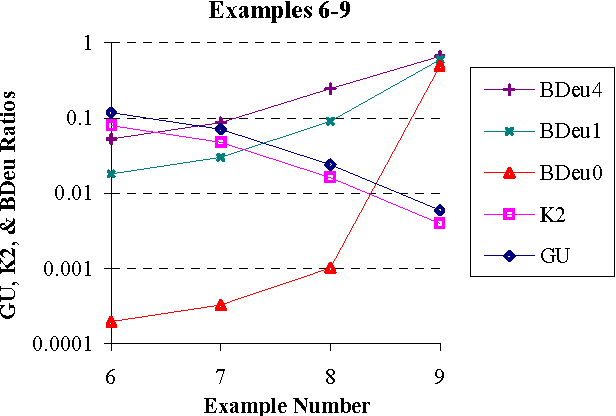
We introduce a new Bayesian network (BN) scoring metric called the Global Uniform (GU) metric. This metric is based on a particular type of default parameter prior. Such priors may be useful when a BN developer is not willing or able to specify domain-specific parameter priors. The GU parameter prior specifies that every prior joint probability distribution P consistent with a BN structure S is considered to be equally likely. Distribution P is consistent with S if P includes just the set of independence relations defined by S. We show that the GU metric addresses some undesirable behavior of the BDeu and K2 Bayesian network scoring metrics, which also use particular forms of default parameter priors. A closed form formula for computing GU for special classes of BNs is derived. Efficiently computing GU for an arbitrary BN remains an open problem.