A Bayesian Multiresolution Independence Test for Continuous Variables
Paper and Code
Jan 10, 2013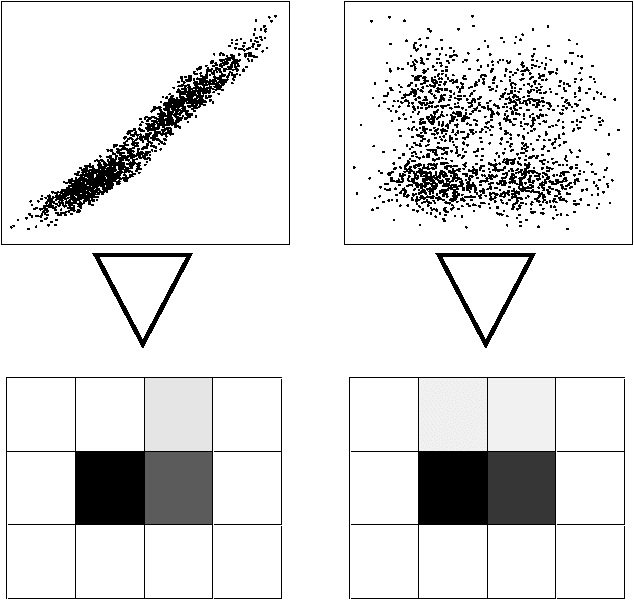

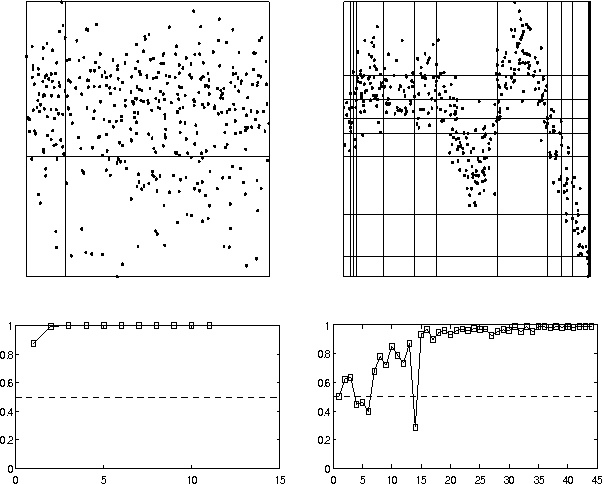
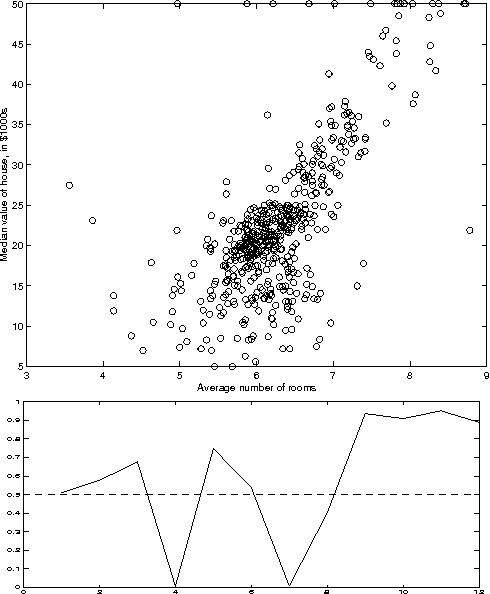
In this paper we present a method ofcomputing the posterior probability ofconditional independence of two or morecontinuous variables from data,examined at several resolutions. Ourapproach is motivated by theobservation that the appearance ofcontinuous data varies widely atvarious resolutions, producing verydifferent independence estimatesbetween the variablesinvolved. Therefore, it is difficultto ascertain independence withoutexamining data at several carefullyselected resolutions. In our paper, weaccomplish this using the exactcomputation of the posteriorprobability of independence, calculatedanalytically given a resolution. Ateach examined resolution, we assume amultinomial distribution with Dirichletpriors for the discretized tableparameters, and compute the posteriorusing Bayesian integration. Acrossresolutions, we use a search procedureto approximate the Bayesian integral ofprobability over an exponential numberof possible histograms. Our methodgeneralizes to an arbitrary numbervariables in a straightforward manner.The test is suitable for Bayesiannetwork learning algorithms that useindependence tests to infer the networkstructure, in domains that contain anymix of continuous, ordinal andcategorical variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge