A Bandit Approach to Maximum Inner Product Search
Paper and Code
Dec 15, 2018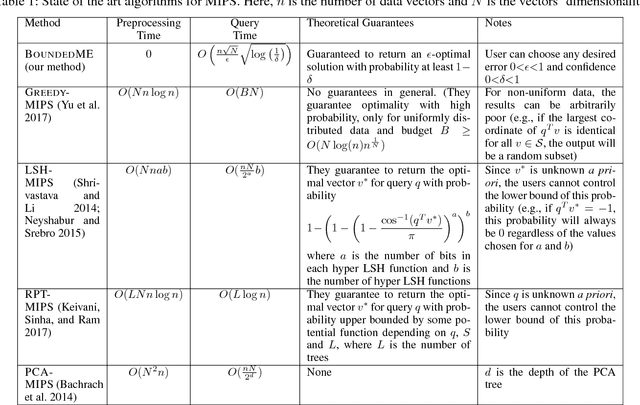
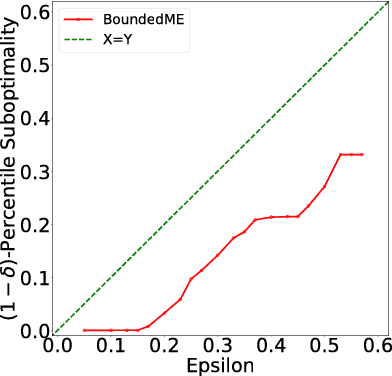
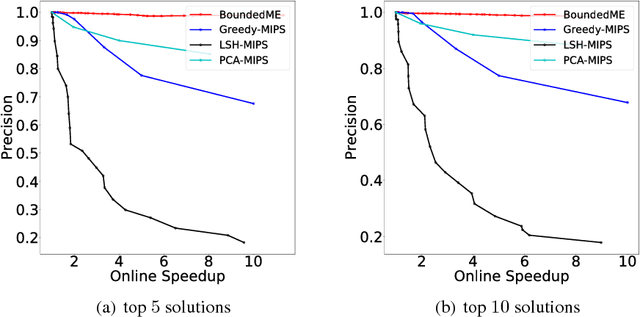
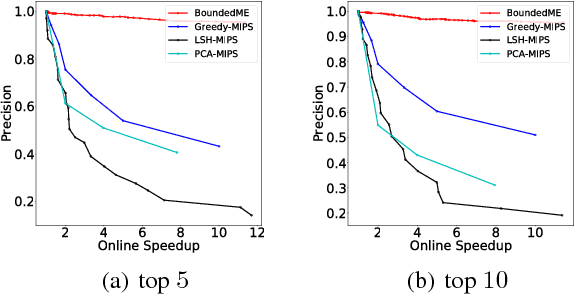
There has been substantial research on sub-linear time approximate algorithms for Maximum Inner Product Search (MIPS). To achieve fast query time, state-of-the-art techniques require significant preprocessing, which can be a burden when the number of subsequent queries is not sufficiently large to amortize the cost. Furthermore, existing methods do not have the ability to directly control the suboptimality of their approximate results with theoretical guarantees. In this paper, we propose the first approximate algorithm for MIPS that does not require any preprocessing, and allows users to control and bound the suboptimality of the results. We cast MIPS as a Best Arm Identification problem, and introduce a new bandit setting that can fully exploit the special structure of MIPS. Our approach outperforms state-of-the-art methods on both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge