Fuzzy Labeling Semantics for Quantitative Argumentation

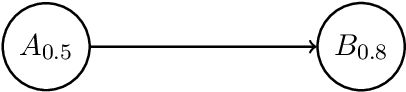
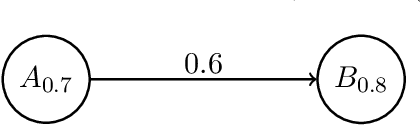
The topic of evaluating argument strength in various quantitative argumentation systems has received increasing attention in the field of abstract argumentation. However, the existing gradual semantics on argument strength considers acceptability degree alone, which may be not sufficient to evaluate arguments in practical scenarios. To adopt a richer characterization for argument strength in real-world applications, we provide a novel quantitative method called fuzzy labeling for fuzzy argumentation systems. For fuzzy labeling, the argument strength is represented as a triple consisting of acceptability, rejectability, and undecidability degree. With a richer scale, it sheds new light on argument strength and gives us a deeper understanding into status of arguments. For the purpose of evaluating arguments, we provide a new way to establish gradual semantics by fuzzy labeling, which is crucial in the evaluation process. We first investigate the rationality postulates of fuzzy labeling, which are important for explaining the rationality of new semantics taking into account the acceptability, rejectability and undecidability degree together. We then propose a set of fuzzy labeling semantics and prove some important properties which are crucial for comparing, understanding and applying semantics.

The SCC-recursiveness Principle in Fuzzy Argumentation Frameworks

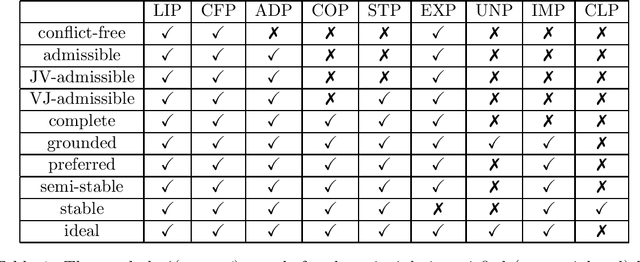
Dung's abstract argumentation theory plays a guiding role in the field of formal argumentation. The properties of argumentation semantics have been deeply explored in the previous literature. The SCC-recursiveness principle is a property of the extensions which relies on the graph-theoretical notion of strongly connected components. It provides a general recursive schema for argumentation semantics, which is an efficient and incremental algorithm for computing the argumentation semantics. However, in argumentation frameworks with uncertain arguments and uncertain attack relation, the SCC-recursive theory is absence. This paper is an exploration of the SCC-recursive theory in fuzzy argumentation frameworks (FAFs), which add numbers as fuzzy degrees to the arguments and attacks. In this paper, in order to extend the SCC-recursiveness principle to FAFs, we first modify the reinstatement principle and directionality principle to fit the FAFs. Then the SCC-recursiveness principle in FAFs is formalized by the modified principles. Additionally, some illustrating examples show that the SCC-recursiveness principle also provides an efficient and incremental algorithm for simplify the computation of argumentation semantics in FAFs.