Fuzzy Labeling Semantics for Quantitative Argumentation

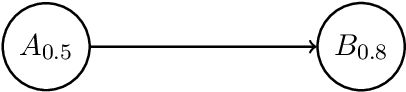
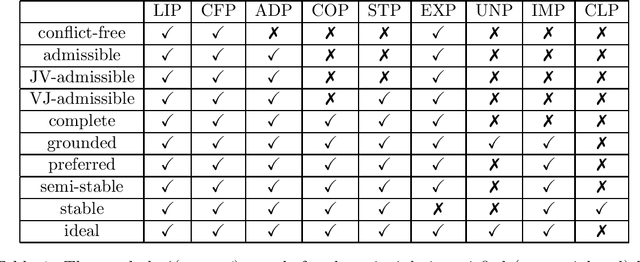
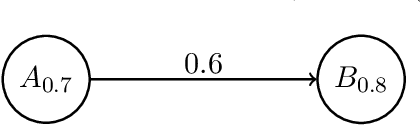
The topic of evaluating argument strength in various quantitative argumentation systems has received increasing attention in the field of abstract argumentation. However, the existing gradual semantics on argument strength considers acceptability degree alone, which may be not sufficient to evaluate arguments in practical scenarios. To adopt a richer characterization for argument strength in real-world applications, we provide a novel quantitative method called fuzzy labeling for fuzzy argumentation systems. For fuzzy labeling, the argument strength is represented as a triple consisting of acceptability, rejectability, and undecidability degree. With a richer scale, it sheds new light on argument strength and gives us a deeper understanding into status of arguments. For the purpose of evaluating arguments, we provide a new way to establish gradual semantics by fuzzy labeling, which is crucial in the evaluation process. We first investigate the rationality postulates of fuzzy labeling, which are important for explaining the rationality of new semantics taking into account the acceptability, rejectability and undecidability degree together. We then propose a set of fuzzy labeling semantics and prove some important properties which are crucial for comparing, understanding and applying semantics.

View-Invariant Recognition of Action Style Self-Dissimilarity

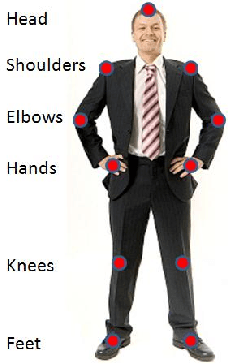
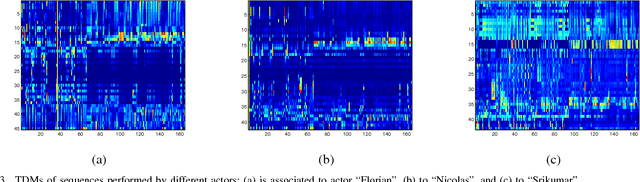
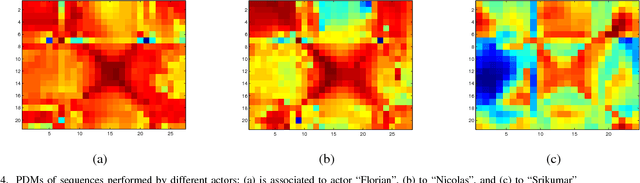
Self-similarity was recently introduced as a measure of inter-class congruence for classification of actions. Herein, we investigate the dual problem of intra-class dissimilarity for classification of action styles. We introduce self-dissimilarity matrices that discriminate between same actions performed by different subjects regardless of viewing direction and camera parameters. We investigate two frameworks using these invariant style dissimilarity measures based on Principal Component Analysis (PCA) and Fisher Discriminant Analysis (FDA). Extensive experiments performed on IXMAS dataset indicate remarkably good discriminant characteristics for the proposed invariant measures for gender recognition from video data.

An Invariant Model of the Significance of Different Body Parts in Recognizing Different Actions

In this paper, we show that different body parts do not play equally important roles in recognizing a human action in video data. We investigate to what extent a body part plays a role in recognition of different actions and hence propose a generic method of assigning weights to different body points. The approach is inspired by the strong evidence in the applied perception community that humans perform recognition in a foveated manner, that is they recognize events or objects by only focusing on visually significant aspects. An important contribution of our method is that the computation of the weights assigned to body parts is invariant to viewing directions and camera parameters in the input data. We have performed extensive experiments to validate the proposed approach and demonstrate its significance. In particular, results show that considerable improvement in performance is gained by taking into account the relative importance of different body parts as defined by our approach.

Canonical Logic Programs are Succinctly Incomparable with Propositional Formulas

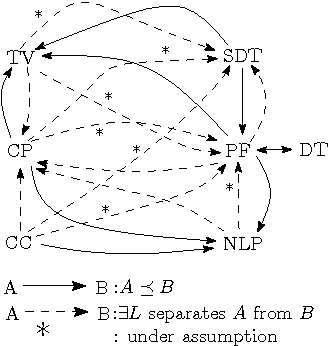
\emph{Canonical (logic) programs} (CP) refer to normal logic programs augmented with connective $not\ not$. In this paper we address the question of whether CP are \emph{succinctly incomparable} with \emph{propositional formulas} (PF). Our main result shows that the PARITY problem, which can be polynomially represented in PF but \emph{only} has exponential representations in CP. In other words, PARITY \emph{separates} PF from CP. Simply speaking, this means that exponential size blowup is generally inevitable when translating a set of formulas in PF into an equivalent program in CP (without introducing new variables). Furthermore, since it has been shown by Lifschitz and Razborov that there is also a problem that separates CP from PF (assuming $\mathsf{P}\nsubseteq \mathsf{NC^1/poly}$), it follows that CP and PF are indeed succinctly incomparable. From the view of the theory of computation, the above result may also be considered as the separation of two \emph{models of computation}, i.e., we identify a language in $\mathsf{NC^1/poly}$ which is not in the set of languages computable by polynomial size CP programs.

Proof System for Plan Verification under 0-Approximation Semantics

In this paper a proof system is developed for plan verification problems $\{X\}c\{Y\}$ and $\{X\}c\{KW p\}$ under 0-approximation semantics for ${\mathcal A}_K$. Here, for a plan $c$, two sets $X,Y$ of fluent literals, and a literal $p$, $\{X\}c\{Y\}$ (resp. $\{X\}c\{KW p\}$) means that all literals of $Y$ become true (resp. $p$ becomes known) after executing $c$ in any initial state in which all literals in $X$ are true.Then, soundness and completeness are proved. The proof system allows verifying plans and generating plans as well.