Zoltán Kovács
The Private University College of Education of the Diocese of Linz, Austria
Automated proving in planar geometry based on the complex number identity method and elimination
Nov 18, 2025Abstract:We improve the complex number identity proving method to a fully automated procedure, based on elimination ideals. By using declarative equations or rewriting each real-relational hypothesis $h_i$ to $h_i-r_i$, and the thesis $t$ to $t-r$, clearing the denominators and introducing an extra expression with a slack variable, we eliminate all free and relational point variables. From the obtained ideal $I$ in $\mathbb{Q}[r,r_1,r_2,\ldots]$ we can find a conclusive result. It plays an important role that if $r_1,r_2,\ldots$ are real, $r$ must also be real if there is a linear polynomial $p(r)\in I$, unless division by zero occurs when expressing $r$. Our results are presented in Mathematica, Maple and in a new version of the Giac computer algebra system. Finally, we present a prototype of the automated procedure in an experimental version of the dynamic geometry software GeoGebra.
Showing Proofs, Assessing Difficulty with GeoGebra Discovery
Jan 22, 2024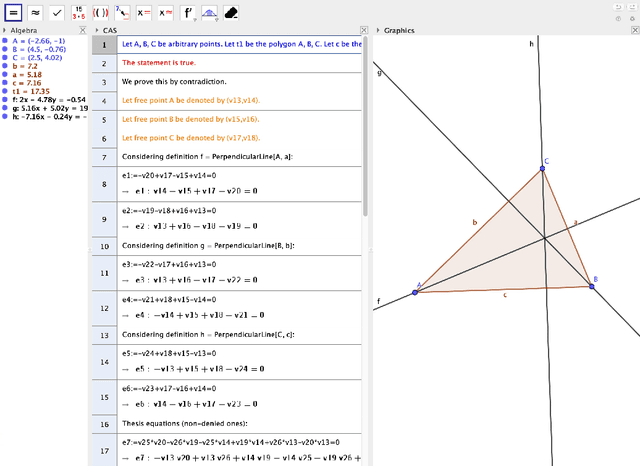
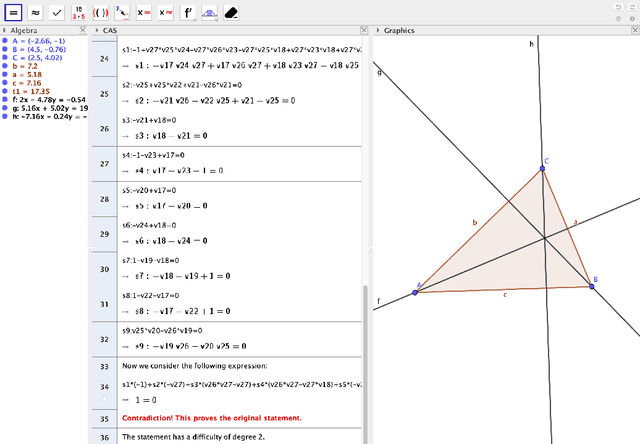

Abstract:In our contribution we describe some on-going improvements concerning the Automated Reasoning Tools developed in GeoGebra Discovery, providing different examples of the performance of these new features. We describe the new ShowProof command, that outputs both the sequence of the different steps performed by GeoGebra Discovery to confirm a certain statement, as well as a number intending to grade the difficulty or interest of the assertion. The proposal of this assessment measure, involving the comparison of the expression of the thesis (or conclusion) as a combination of the hypotheses, will be developed.
* In Proceedings ADG 2023, arXiv:2401.10725
Using Java Geometry Expert as Guide in the Preparations for Math Contests
Jan 22, 2024Abstract:We give an insight into Java Geometry Expert (JGEX) in use in a school context, focusing on the Austrian school system. JGEX can offer great support in some classroom situations, especially for solving mathematical competition tasks. Also, we discuss some limitations of the program.
* In Proceedings ADG 2023, arXiv:2401.10725
Solving Some Geometry Problems of the Náboj 2023 Contest with Automated Deduction in GeoGebra Discovery
Jan 22, 2024



Abstract:In this article, we solve some of the geometry problems of the N\'aboj 2023 competition with the help of a computer, using examples that the software tool GeoGebra Discovery can calculate. In each case, the calculation requires symbolic computations. We analyze the difficulty of feeding the problem into the machine and set further goals to make the problems of this type of contests even more tractable in the future.
* In Proceedings ADG 2023, arXiv:2401.10725
The Locus Story of a Rocking Camel in a Medical Center in the City of Freistadt
Jan 22, 2024
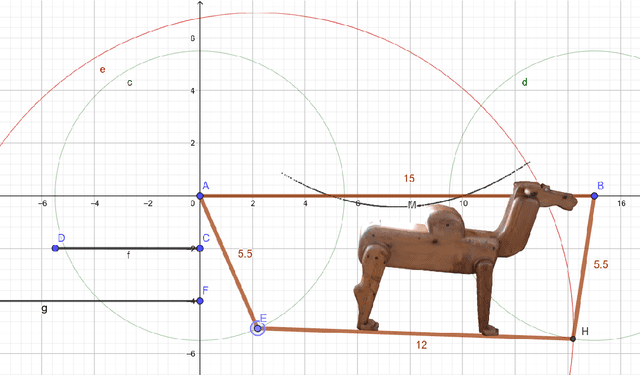


Abstract:We give an example of automated geometry reasoning for an imaginary classroom project by using the free software package GeoGebra Discovery. The project is motivated by a publicly available toy, a rocking camel, installed at a medical center in Upper Austria. We explain how the process of a false conjecture, experimenting, modeling, a precise mathematical setup, and then a proof by automated reasoning could help extend mathematical knowledge at secondary school level and above.
* In Proceedings ADG 2023, arXiv:2401.10725
Solving with GeoGebra Discovery an Austrian Mathematics Olympiad problem: Lessons Learned
Jan 22, 2024



Abstract:We address, through the automated reasoning tools in GeoGebra Discovery, a problem from a regional phase of the Austrian Mathematics Olympiad 2023. Trying to solve this problem gives rise to four different kind of feedback: the almost instantaneous, automated solution of the proposed problem; the measure of its complexity, according to some recent proposals; the automated discovery of a generalization of the given assertion, showing that the same statement is true over more general polygons than those mentioned in the problem; and the difficulties associated to the analysis of the surprising and involved high number of degenerate cases that appear when using the LocusEquation command in this problem. In our communication we will describe and reflect on these diverse issues, enhancing its exemplar role for showing some of the advantages, problems, and current fields of development of GeoGebra Discovery.
* In Proceedings ADG 2023, arXiv:2401.10725
Proceedings 14th International Conference on Automated Deduction in Geometry
Jan 19, 2024Abstract:ADG is a forum to exchange ideas and views, to present research results and progress, and to demonstrate software tools at the intersection between geometry and automated deduction. The conference is held every two years. The previous editions of ADG were held in Hagenberg in 2021 (online, postponed from 2020 due to COVID-19), Nanning in 2018, Strasbourg in 2016, Coimbra in 2014, Edinburgh in 2012, Munich in 2010, Shanghai in 2008, Pontevedra in 2006, Gainesville in 2004, Hagenberg in 2002, Zurich in 2000, Beijing in 1998, and Toulouse in 1996. The 14th edition, ADG 2023, was held in Belgrade, Serbia, in September 20-22, 2023. This edition of ADG had an additional special focus topic, Deduction in Education. Invited Speakers: Julien Narboux, University of Strasbourg, France "Formalisation, arithmetization and automatisation of geometry"; Filip Mari\'c, University of Belgrade, Serbia, "Automatization, formalization and visualization of hyperbolic geometry"; Zlatan Magajna, University of Ljubljana, Slovenia, "Workshop OK Geometry"
Proceedings of the 13th International Conference on Automated Deduction in Geometry
Dec 28, 2021Abstract:Automated Deduction in Geometry (ADG) is a forum to exchange ideas and views, to present research results and progress, and to demonstrate software tools at the intersection between geometry and automated deduction. Relevant topics include (but are not limited to): polynomial algebra, invariant and coordinate-free methods; probabilistic, synthetic, and logic approaches, techniques for automated geometric reasoning from discrete mathematics, combinatorics, and numerics; interactive theorem proving in geometry; symbolic and numeric methods for geometric computation, geometric constraint solving, automated generation/reasoning and manipulation with diagrams; design and implementation of geometry software, automated theorem provers, special-purpose tools, experimental studies; applications of ADG in mechanics, geometric modelling, CAGD/CAD, computer vision, robotics and education. Traditionally, the ADG conference is held every two years. The previous editions of ADG were held in Nanning in 2018, Strasbourg in 2016, Coimbra in 2014, Edinburgh in 2012, Munich in 2010, Shanghai in 2008, Pontevedra in 2006, Gainesville in 2004, Hagenberg in 2002, Zurich in 2000, Beijing in 1998, and Toulouse in 1996. The 13th edition of ADG was supposed to be held in 2020 in Hagenberg, Austria, but due to the COVID-19 pandemic, it was postponed for 2021, and held online (still hosted by RISC Institute, Hagenberg, Austria), September 15-17, 2021 (https://www.risc.jku.at/conferences/adg2021).
Towards Automated Discovery of Geometrical Theorems in GeoGebra
Jul 24, 2020



Abstract:We describe a prototype of a new experimental GeoGebra command and tool Discover that analyzes geometric figures for salient patterns, properties, and theorems. This tool is a basic implementation of automated discovery in elementary planar geometry. The paper focuses on the mathematical background of the implementation, as well as methods to avoid combinatorial explosion when storing the interesting properties of a geometric figure.
Towards a Geometry Automated Provers Competition
Feb 28, 2020Abstract:The geometry automated theorem proving area distinguishes itself by a large number of specific methods and implementations, different approaches (synthetic, algebraic, semi-synthetic) and different goals and applications (from research in the area of artificial intelligence to applications in education). Apart from the usual measures of efficiency (e.g. CPU time), the possibility of visual and/or readable proofs is also an expected output against which the geometry automated theorem provers (GATP) should be measured. The implementation of a competition between GATP would allow to create a test bench for GATP developers to improve the existing ones and to propose new ones. It would also allow to establish a ranking for GATP that could be used by "clients" (e.g. developers of educational e-learning systems) to choose the best implementation for a given intended use.
* In Proceedings ThEdu'19, arXiv:2002.11895
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge