Showing Proofs, Assessing Difficulty with GeoGebra Discovery

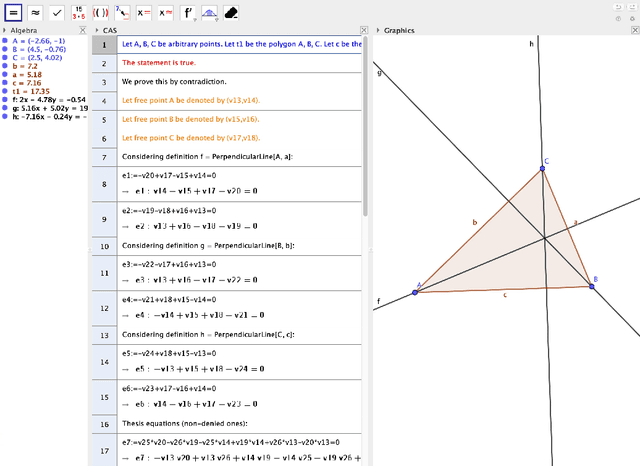
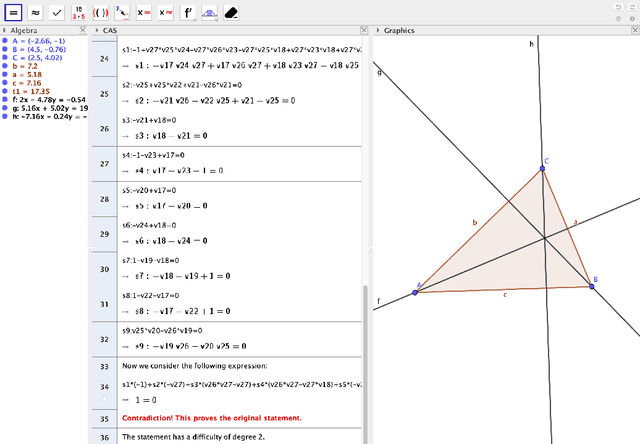
In our contribution we describe some on-going improvements concerning the Automated Reasoning Tools developed in GeoGebra Discovery, providing different examples of the performance of these new features. We describe the new ShowProof command, that outputs both the sequence of the different steps performed by GeoGebra Discovery to confirm a certain statement, as well as a number intending to grade the difficulty or interest of the assertion. The proposal of this assessment measure, involving the comparison of the expression of the thesis (or conclusion) as a combination of the hypotheses, will be developed.

Solving with GeoGebra Discovery an Austrian Mathematics Olympiad problem: Lessons Learned

We address, through the automated reasoning tools in GeoGebra Discovery, a problem from a regional phase of the Austrian Mathematics Olympiad 2023. Trying to solve this problem gives rise to four different kind of feedback: the almost instantaneous, automated solution of the proposed problem; the measure of its complexity, according to some recent proposals; the automated discovery of a generalization of the given assertion, showing that the same statement is true over more general polygons than those mentioned in the problem; and the difficulties associated to the analysis of the surprising and involved high number of degenerate cases that appear when using the LocusEquation command in this problem. In our communication we will describe and reflect on these diverse issues, enhancing its exemplar role for showing some of the advantages, problems, and current fields of development of GeoGebra Discovery.

Detecting truth, just on parts

We introduce and discuss, through a computational algebraic geometry approach, the automatic reasoning handling of propositions that are simultaneously true and false over some relevant collections of instances. A rigorous, algorithmic criterion is presented for detecting such cases, and its performance is exemplified through the implementation of this test on the dynamic geometry program GeoGebra.