Merit-based Fair Combinatorial Semi-Bandit with Unrestricted Feedback Delays

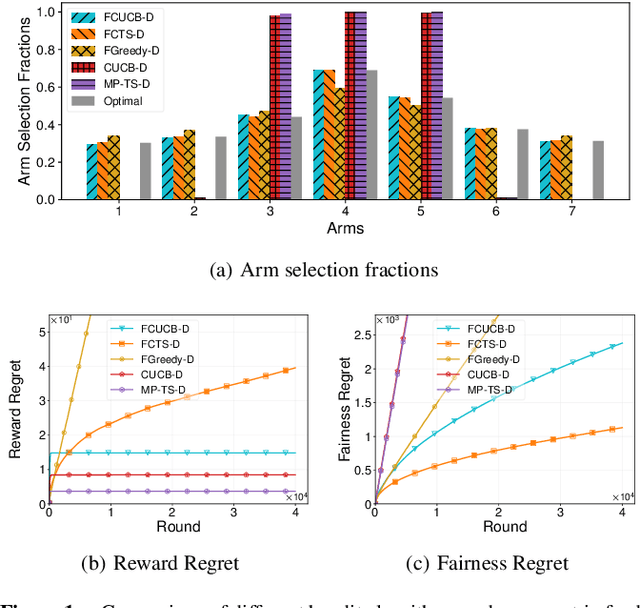
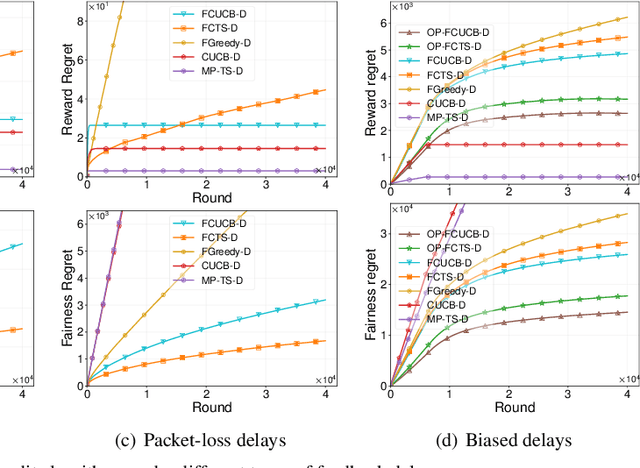
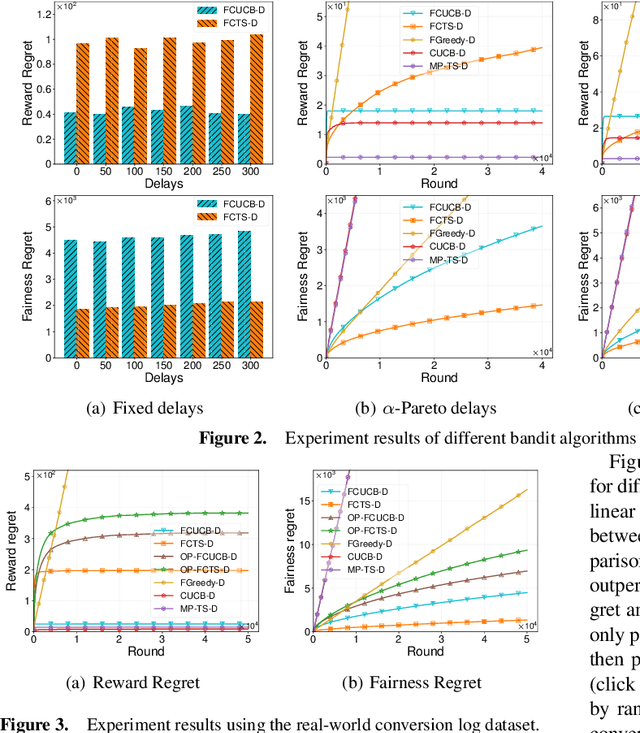
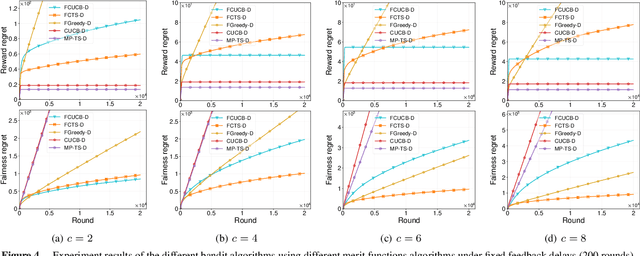
We study the stochastic combinatorial semi-bandit problem with unrestricted feedback delays under merit-based fairness constraints. This is motivated by applications such as crowdsourcing, and online advertising, where immediate feedback is not immediately available and fairness among different choices (or arms) is crucial. We consider two types of unrestricted feedback delays: reward-independent delays where the feedback delays are independent of the rewards, and reward-dependent delays where the feedback delays are correlated with the rewards. Furthermore, we introduce merit-based fairness constraints to ensure a fair selection of the arms. We define the reward regret and the fairness regret and present new bandit algorithms to select arms under unrestricted feedback delays based on their merits. We prove that our algorithms all achieve sublinear expected reward regret and expected fairness regret, with a dependence on the quantiles of the delay distribution. We also conduct extensive experiments using synthetic and real-world data and show that our algorithms can fairly select arms with different feedback delays.

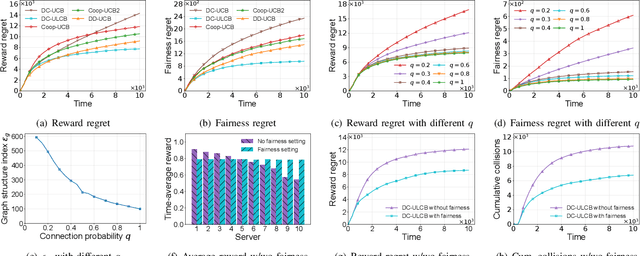
Fair Distributed Cooperative Bandit Learning on Networks for Intelligent Internet of Things Systems (Technical Report)

In intelligent Internet of Things (IoT) systems, edge servers within a network exchange information with their neighbors and collect data from sensors to complete delivered tasks. In this paper, we propose a multiplayer multi-armed bandit model for intelligent IoT systems to facilitate data collection and incorporate fairness considerations. In our model, we establish an effective communication protocol that helps servers cooperate with their neighbors. Then we design a distributed cooperative bandit algorithm, DC-ULCB, enabling servers to collaboratively select sensors to maximize data rates while maintaining fairness in their choices. We conduct an analysis of the reward regret and fairness regret of DC-ULCB, and prove that both regrets have logarithmic instance-dependent upper bounds. Additionally, through extensive simulations, we validate that DC-ULCB outperforms existing algorithms in maximizing reward and ensuring fairness.