Zhizhao Wen
Dynamic Analysis of Nonlinear Civil Engineering Structures using Artificial Neural Network with Adaptive Training
Nov 21, 2021
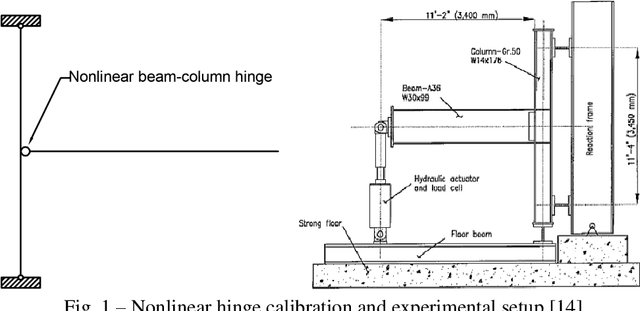
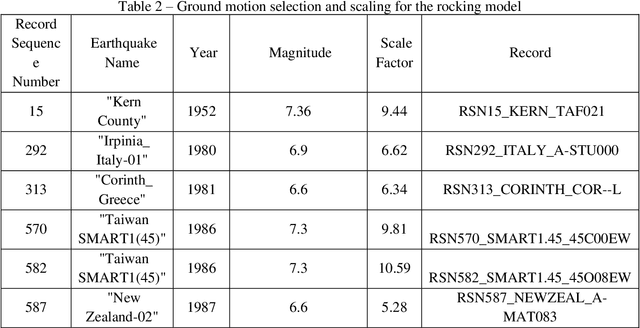

Abstract:Dynamic analysis of structures subjected to earthquake excitation is a time-consuming process, particularly in the case of extremely small time step required, or in the presence of high geometric and material nonlinearity. Performing parametric studies in such cases is even more tedious. The advancement of computer graphics hardware in recent years enables efficient training of artificial neural networks that are well-known to be capable of learning highly nonlinear mappings. In this study, artificial neural networks are developed with adaptive training algorithms, which enables automatic nodes generation and layers addition. The hyperbolic tangent function is selected as the activation function. Stochastic Gradient Descent and Back Propagation algorithms are adopted to train the networks. The neural networks initiate with a small number of hidden layers and nodes. During training, the performance of the network is continuously tracked, and new nodes or layers are added to the hidden layers if the neural network reaches its capacity. At the end of the training process, the network with appropriate architecture is automatically formed. The performance of the networks has been validated for inelastic shear frames, as well as rocking structures, of which both are first built in finite element program for dynamic analysis to generate training data. Results have shown the developed networks can successfully predict the time-history response of the shear frame and the rock structure subjected to real ground motion records. The efficiency of the proposed neural networks is also examined, which shows the computational time can be reduced by 43% by the neural networks method than FE models. This indicates the trained networks can be utilized to generate rocking spectrums of structures more efficiently which demands a large number of time-history analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge