Generative Bayesian Spectrum Cartography: Unified Reconstruction and Active Sensing via Diffusion Models

High-fidelity spectrum cartography is pivotal for spectrum management and wireless situational awareness, yet it remains a challenging ill-posed inverse problem due to the sparsity and irregularity of observations. Furthermore, existing approaches often decouple reconstruction from sensing, lacking a principled mechanism for informative sampling. To address these limitations, this paper proposes a unified diffusion-based Bayesian framework that jointly addresses spectrum reconstruction and active sensing. We formulate the reconstruction task as a conditional generation process driven by a learned diffusion prior. Specifically, we derive tractable, closed-form posterior transition kernels for the reverse diffusion process, which enforce consistency with both linear Gaussian and non-linear quantized measurements. Leveraging the intrinsic probabilistic nature of diffusion models, we further develop an uncertainty-aware active sampling strategy. This strategy quantifies reconstruction uncertainty to adaptively guide sensing agents toward the most informative locations, thereby maximizing spectral efficiency. Extensive experiments demonstrate that the proposed framework significantly outperforms state-of-the-art interpolation, sparsity-based, and deep learning baselines in terms of reconstruction accuracy, sampling efficiency, and robustness to low-bit quantization.

A deep reinforcement learning approach for real-time demand-responsive railway rescheduling to mitigate station overcrowding using mobile data

Real-time railway rescheduling is a timely and flexible technique to automatically alter the operation schedule in response to time-varying conditions. Current research lacks data-driven approaches that capture real-time passenger mobility during railway disruptions, relying mostly on OD-based data and model-based methods for estimating demands of trains. Meanwhile, the schedule-updating principles for a long-term disruption overlook the uneven distribution of demand over time. To fill this gap, this paper proposes a demand-responsive approach by inferring real-world passenger mobility from mobile data (MD) to facilitate real-time rescheduling. Unlike network-level approaches, this paper focuses on a heavy-demand station upstream of the disrupted area. The objective is to reschedule all trains on multiple routes passing through this target station, which have been affected by a severe emergency event such as a natural disaster. Particular attention should be given to avoiding the accumulation of overcrowded passengers at this station, to prevent additional accidents arising from overcrowding. This research addresses the challenges associated with this scenario, including the dynamics of arriving and leaving of passengers, station overcrowding, rolling stock shortage, open-ended disruption duration, integrated rescheduling on multiple routes, and delays due to detours. A deep reinforcement learning (DRL) framework is proposed to determine the optimal rescheduled timetable, route stops, and rolling stock allocation, while considering real-time demand satisfaction, station overcrowding, train capacity utilization, and headway safety.

Probability Paths and the Structure of Predictions over Time

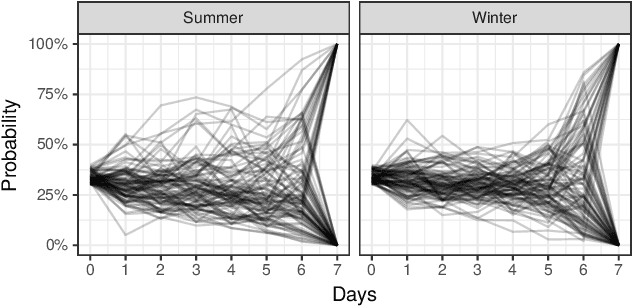
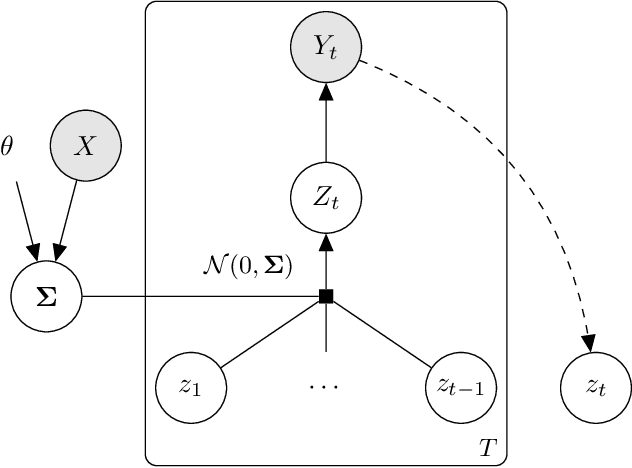
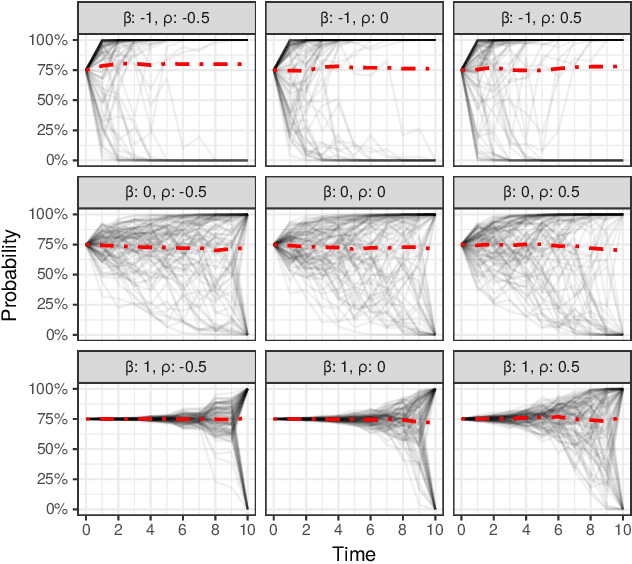
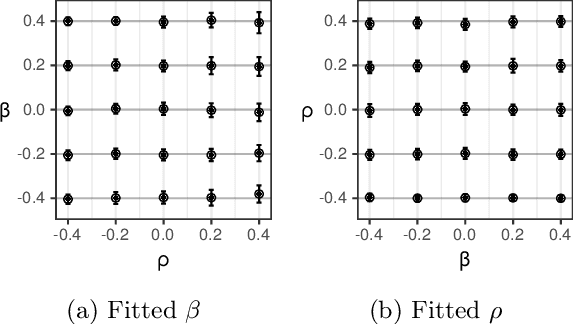
In settings ranging from weather forecasts to political prognostications to financial projections, probability estimates of future binary outcomes often evolve over time. For example, the estimated likelihood of rain on a specific day changes by the hour as new information becomes available. Given a collection of such probability paths, we introduce a Bayesian framework -- which we call the Gaussian latent information martingale, or GLIM -- for modeling the structure of dynamic predictions over time. Suppose, for example, that the likelihood of rain in a week is 50%, and consider two hypothetical scenarios. In the first, one expects the forecast is equally likely to become either 25% or 75% tomorrow; in the second, one expects the forecast to stay constant for the next several days. A time-sensitive decision-maker might select a course of action immediately in the latter scenario, but may postpone their decision in the former, knowing that new information is imminent. We model these trajectories by assuming predictions update according to a latent process of information flow, which is inferred from historical data. In contrast to general methods for time series analysis, this approach preserves the martingale structure of probability paths and better quantifies future uncertainties around probability paths. We show that GLIM outperforms three popular baseline methods, producing better estimated posterior probability path distributions measured by three different metrics. By elucidating the dynamic structure of predictions over time, we hope to help individuals make more informed choices.