Learning Sparse Approximate Inverse Preconditioners for Conjugate Gradient Solvers on GPUs

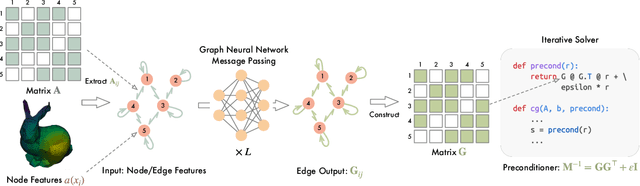
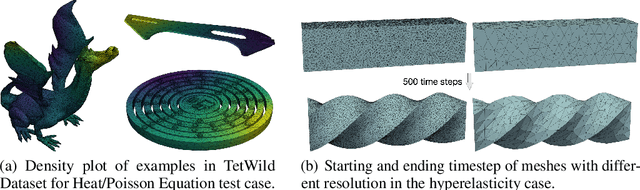
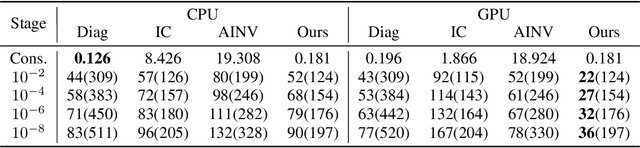
The conjugate gradient solver (CG) is a prevalent method for solving symmetric and positive definite linear systems Ax=b, where effective preconditioners are crucial for fast convergence. Traditional preconditioners rely on prescribed algorithms to offer rigorous theoretical guarantees, while limiting their ability to exploit optimization from data. Existing learning-based methods often utilize Graph Neural Networks (GNNs) to improve the performance and speed up the construction. However, their reliance on incomplete factorization leads to significant challenges: the associated triangular solve hinders GPU parallelization in practice, and introduces long-range dependencies which are difficult for GNNs to model. To address these issues, we propose a learning-based method to generate GPU-friendly preconditioners, particularly using GNNs to construct Sparse Approximate Inverse (SPAI) preconditioners, which avoids triangular solves and requires only two matrix-vector products at each CG step. The locality of matrix-vector product is compatible with the local propagation mechanism of GNNs. The flexibility of GNNs also allows our approach to be applied in a wide range of scenarios. Furthermore, we introduce a statistics-based scale-invariant loss function. Its design matches CG's property that the convergence rate depends on the condition number, rather than the absolute scale of A, leading to improved performance of the learned preconditioner. Evaluations on three PDE-derived datasets and one synthetic dataset demonstrate that our method outperforms standard preconditioners (Diagonal, IC, and traditional SPAI) and previous learning-based preconditioners on GPUs. We reduce solution time on GPUs by 40%-53% (68%-113% faster), along with better condition numbers and superior generalization performance. Source code available at https://github.com/Adversarr/LearningSparsePreconditioner4GPU

Modeling the Multivariate Relationship with Contextualized Representations for Effective Human-Object Interaction Detection

Human-Object Interaction (HOI) detection aims to simultaneously localize human-object pairs and recognize their interactions. While recent two-stage approaches have made significant progress, they still face challenges due to incomplete context modeling. In this work, we introduce a Contextualized Representation Learning Network that integrates both affordance-guided reasoning and contextual prompts with visual cues to better capture complex interactions. We enhance the conventional HOI detection framework by expanding it beyond simple human-object pairs to include multivariate relationships involving auxiliary entities like tools. Specifically, we explicitly model the functional role (affordance) of these auxiliary objects through triplet structures <human, tool, object>. This enables our model to identify tool-dependent interactions such as 'filling'. Furthermore, the learnable prompt is enriched with instance categories and subsequently integrated with contextual visual features using an attention mechanism. This process aligns language with image content at both global and regional levels. These contextualized representations equip the model with enriched relational cues for more reliable reasoning over complex, context-dependent interactions. Our proposed method demonstrates superior performance on both the HICO-Det and V-COCO datasets in most scenarios. Codes will be released upon acceptance.

DQEN: Dual Query Enhancement Network for DETR-based HOI Detection

Human-Object Interaction (HOI) detection focuses on localizing human-object pairs and recognizing their interactions. Recently, the DETR-based framework has been widely adopted in HOI detection. In DETR-based HOI models, queries with clear meaning are crucial for accurately detecting HOIs. However, prior works have typically relied on randomly initialized queries, leading to vague representations that limit the model's effectiveness. Meanwhile, humans in the HOI categories are fixed, while objects and their interactions are variable. Therefore, we propose a Dual Query Enhancement Network (DQEN) to enhance object and interaction queries. Specifically, object queries are enhanced with object-aware encoder features, enabling the model to focus more effectively on humans interacting with objects in an object-aware way. On the other hand, we design a novel Interaction Semantic Fusion module to exploit the HOI candidates that are promoted by the CLIP model. Semantic features are extracted to enhance the initialization of interaction queries, thereby improving the model's ability to understand interactions. Furthermore, we introduce an Auxiliary Prediction Unit aimed at improving the representation of interaction features. Our proposed method achieves competitive performance on both the HICO-Det and the V-COCO datasets. The source code is available at https://github.com/lzzhhh1019/DQEN.

A Fenchel-Young Loss Approach to Data-Driven Inverse Optimization

Data-driven inverse optimization seeks to estimate unknown parameters in an optimization model from observations of optimization solutions. Many existing methods are ineffective in handling noisy and suboptimal solution observations and also suffer from computational challenges. In this paper, we build a connection between inverse optimization and the Fenchel-Young (FY) loss originally designed for structured prediction, proposing a FY loss approach to data-driven inverse optimization. This new approach is amenable to efficient gradient-based optimization, hence much more efficient than existing methods. We provide theoretical guarantees for the proposed method and use extensive simulation and real-data experiments to demonstrate its significant advantage in parameter estimation accuracy, decision error and computational speed.

Learning under Selective Labels with Data from Heterogeneous Decision-makers: An Instrumental Variable Approach

We study the problem of learning with selectively labeled data, which arises when outcomes are only partially labeled due to historical decision-making. The labeled data distribution may substantially differ from the full population, especially when the historical decisions and the target outcome can be simultaneously affected by some unobserved factors. Consequently, learning with only the labeled data may lead to severely biased results when deployed to the full population. Our paper tackles this challenge by exploiting the fact that in many applications the historical decisions were made by a set of heterogeneous decision-makers. In particular, we analyze this setup in a principled instrumental variable (IV) framework. We establish conditions for the full-population risk of any given prediction rule to be point-identified from the observed data and provide sharp risk bounds when the point identification fails. We further propose a weighted learning approach that learns prediction rules robust to the label selection bias in both identification settings. Finally, we apply our proposed approach to a semi-synthetic financial dataset and demonstrate its superior performance in the presence of selection bias.