Zengping Chen
Accelerating Mini-batch SARAH by Step Size Rules
Jun 20, 2019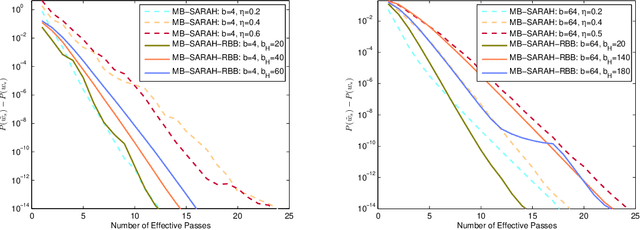
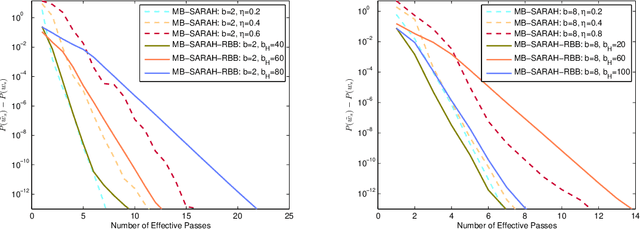


Abstract:StochAstic Recursive grAdient algoritHm (SARAH), originally proposed for convex optimization and also proven to be effective for general nonconvex optimization, has received great attention due to its simple recursive framework for updating stochastic gradient estimates. The performance of SARAH significantly depends on the choice of step size sequence. However, SARAH and its variants often employ a best-tuned step size by mentor, which is time consuming in practice. Motivated by this gap, we proposed a variant of the Barzilai-Borwein (BB) method, referred to as the Random Barzilai-Borwein (RBB) method, to calculate step size for SARAH in the mini-batch setting, thereby leading to a new SARAH method: MB-SARAH-RBB. We prove that MB-SARAH-RBB converges linearly in expectation for strongly convex objective functions. We analyze the complexity of MB-SARAH-RBB and show that it is better than the original method. Numerical experiments on standard data sets indicate that MB-SARAH-RBB outperforms or matches state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge