Zain Hafeez
A Bi-directional Quantum Search Algorithm
Apr 24, 2024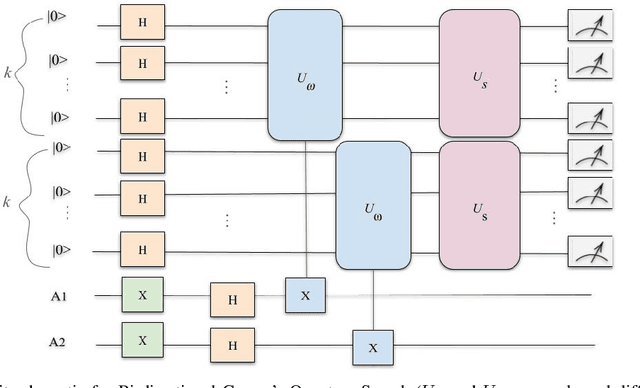
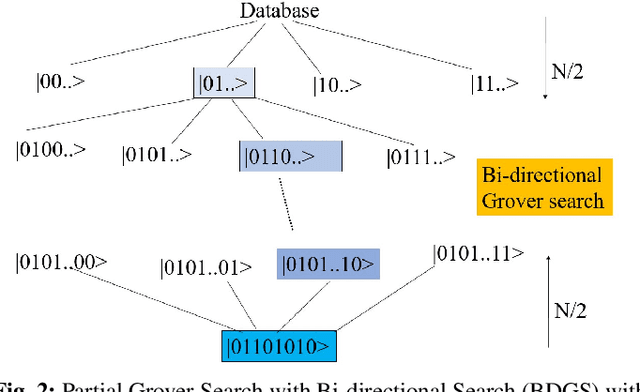
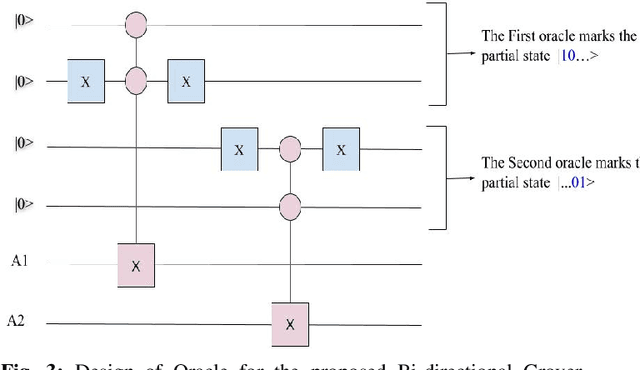
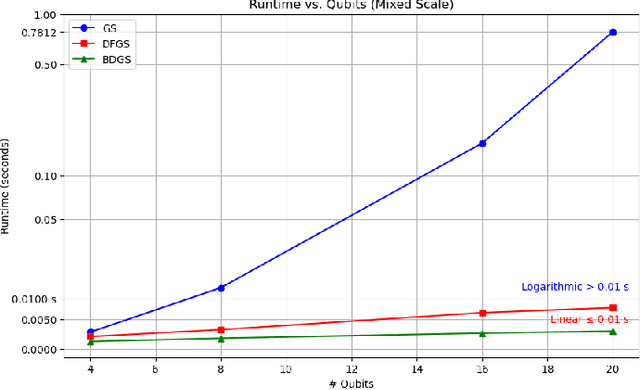
Abstract:Grover's search algorithms, including various partial Grover searches, experience scaling problems as the number of iterations rises with increased qubits, making implementation more computationally expensive. This paper combines Partial Grover's search algorithm and Bi-directional Search to create a fast Grover's quantum search algorithm, referred to as Bi-Directional Grover Search (BDGS). We incorporated a bi-directional search tactic with a partial Grover search, starting from an initial state and a single marked state in parallel. We have shown in this article that our novel approach requires $\frac{\pi}{4\sqrt{2}}\sqrt{N}(1-\sqrt{\frac{1}{b^{r/2k}}})$ iterations over regular Grover Search and Partial Grover Search (PGS), which takes $\frac{\pi}{4}\sqrt{N}\sqrt{1-\frac{1}{b}}$ (here, $N=2^r$ elements, $b$ is the branching factor of partial search, and $k= \lceil\log_2b \rceil$). The proposed BDGS algorithm is benchmarked against the state-of-the-art Depth-First Grover's Search (DFGS) and generic Grover's Search (GS) implementations for $2$ to $20$ qubits and provides promising results. The Qiskit Python implementation of the proposed BDGS algorithm is available on Github (https://github.com/hafeezzwiz21/DFGS-BDGS).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge