Recurrent Neural Operators: Stable Long-Term PDE Prediction

Neural operators have emerged as powerful tools for learning solution operators of partial differential equations. However, in time-dependent problems, standard training strategies such as teacher forcing introduce a mismatch between training and inference, leading to compounding errors in long-term autoregressive predictions. To address this issue, we propose Recurrent Neural Operators (RNOs)-a novel framework that integrates recurrent training into neural operator architectures. Instead of conditioning each training step on ground-truth inputs, RNOs recursively apply the operator to their own predictions over a temporal window, effectively simulating inference-time dynamics during training. This alignment mitigates exposure bias and enhances robustness to error accumulation. Theoretically, we show that recurrent training can reduce the worst-case exponential error growth typical of teacher forcing to linear growth. Empirically, we demonstrate that recurrently trained Multigrid Neural Operators significantly outperform their teacher-forced counterparts in long-term accuracy and stability on standard benchmarks. Our results underscore the importance of aligning training with inference dynamics for robust temporal generalization in neural operator learning.

FBSJNN: A Theoretically Interpretable and Efficiently Deep Learning method for Solving Partial Integro-Differential Equations

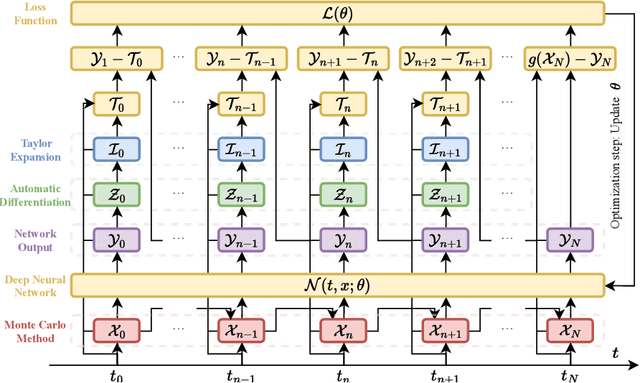
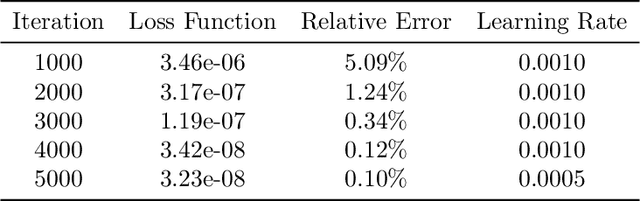
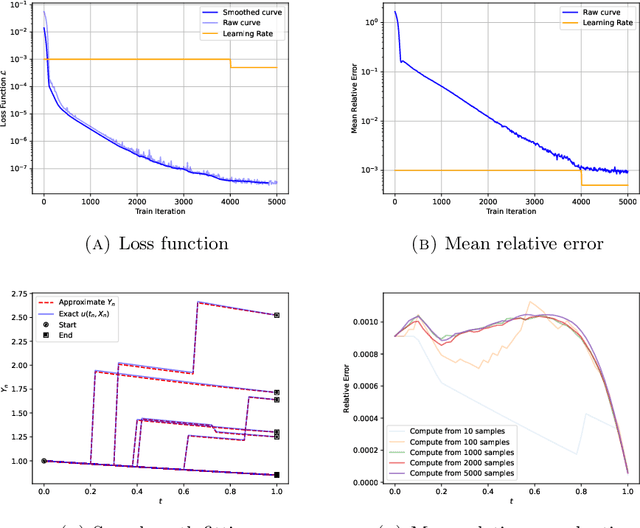
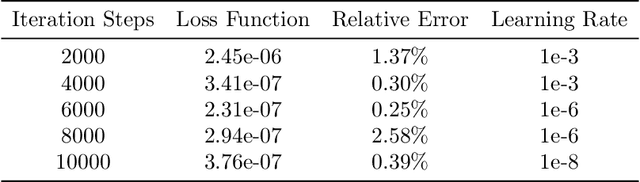
We propose a novel framework for solving a class of Partial Integro-Differential Equations (PIDEs) and Forward-Backward Stochastic Differential Equations with Jumps (FBSDEJs) through a deep learning-based approach. This method, termed the Forward-Backward Stochastic Jump Neural Network (FBSJNN), is both theoretically interpretable and numerically effective. Theoretical analysis establishes the convergence of the numerical scheme and provides error estimates grounded in the universal approximation properties of neural networks. In comparison to existing methods, the key innovation of the FBSJNN framework is that it uses a single neural network to approximate both the solution of the PIDEs and the non-local integral, leveraging Taylor expansion for the latter. This enables the method to reduce the total number of parameters in FBSJNN, which enhances optimization efficiency. Numerical experiments indicate that the FBSJNN scheme can obtain numerical solutions with a relative error on the scale of $10^{-3}$.