Pre-Selection of Independent Binary Features: An Application to Diagnosing Scrapie in Sheep

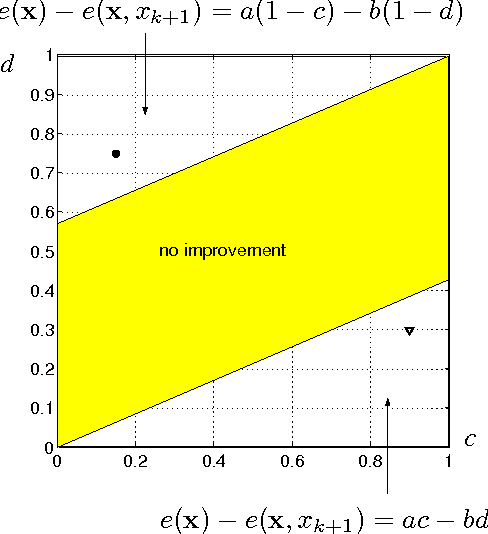
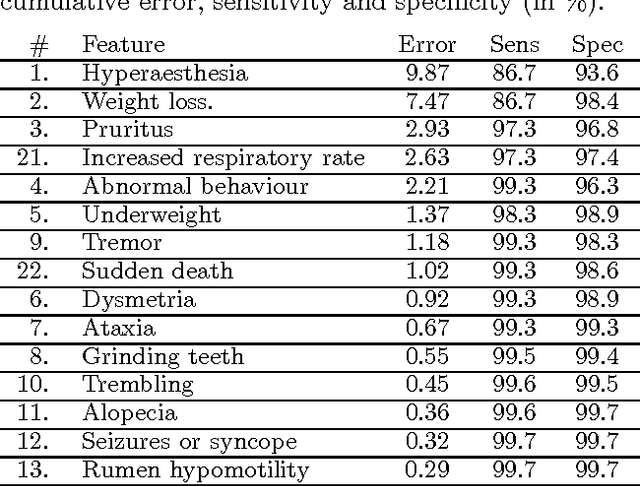
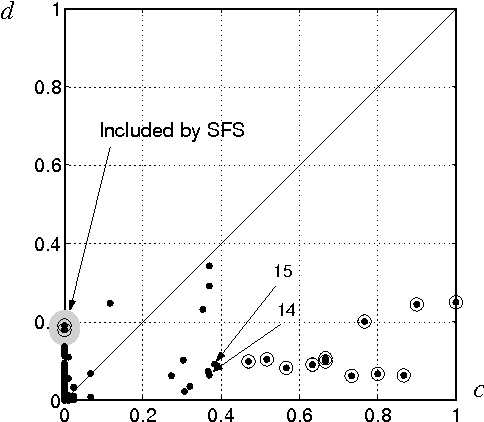
Suppose that the only available information in a multi-class problem are expert estimates of the conditional probabilities of occurrence for a set of binary features. The aim is to select a subset of features to be measured in subsequent data collection experiments. In the lack of any information about the dependencies between the features, we assume that all features are conditionally independent and hence choose the Naive Bayes classifier as the optimal classifier for the problem. Even in this (seemingly trivial) case of complete knowledge of the distributions, choosing an optimal feature subset is not straightforward. We discuss the properties and implementation details of Sequential Forward Selection (SFS) as a feature selection procedure for the current problem. A sensitivity analysis was carried out to investigate whether the same features are selected when the probabilities vary around the estimated values. The procedure is illustrated with a set of probability estimates for Scrapie in sheep.