Random Gradient-Free Optimization in Infinite Dimensional Spaces

In this paper, we propose a random gradient-free method for optimization in infinite dimensional Hilbert spaces, applicable to functional optimization in diverse settings. Though such problems are often solved through finite-dimensional gradient descent over a parametrization of the functions, such as neural networks, an interesting alternative is to instead perform gradient descent directly in the function space by leveraging its Hilbert space structure, thus enabling provable guarantees and fast convergence. However, infinite-dimensional gradients are often hard to compute in practice, hindering the applicability of such methods. To overcome this limitation, our framework requires only the computation of directional derivatives and a pre-basis for the Hilbert space domain, i.e., a linearly-independent set whose span is dense in the Hilbert space. This fully resolves the tractability issue, as pre-bases are much more easily obtained than full orthonormal bases or reproducing kernels -- which may not even exist -- and individual directional derivatives can be easily computed using forward-mode scalar automatic differentiation. We showcase the use of our method to solve partial differential equations à la physics informed neural networks (PINNs), where it effectively enables provable convergence.

Deep Learning and Elicitability for McKean-Vlasov FBSDEs With Common Noise

We present a novel numerical method for solving McKean-Vlasov forward-backward stochastic differential equations (MV-FBSDEs) with common noise, combining Picard iterations, elicitability and deep learning. The key innovation involves elicitability to derive a path-wise loss function, enabling efficient training of neural networks to approximate both the backward process and the conditional expectations arising from common noise - without requiring computationally expensive nested Monte Carlo simulations. The mean-field interaction term is parameterized via a recurrent neural network trained to minimize an elicitable score, while the backward process is approximated through a feedforward network representing the decoupling field. We validate the algorithm on a systemic risk inter-bank borrowing and lending model, where analytical solutions exist, demonstrating accurate recovery of the true solution. We further extend the model to quantile-mediated interactions, showcasing the flexibility of the elicitability framework beyond conditional means or moments. Finally, we apply the method to a non-stationary Aiyagari--Bewley--Huggett economic growth model with endogenous interest rates, illustrating its applicability to complex mean-field games without closed-form solutions.

Reverse-BSDE Monte Carlo

Recently, there has been a growing interest in generative models based on diffusions driven by the empirical robustness of these methods in generating high-dimensional photorealistic images and the possibility of using the vast existing toolbox of stochastic differential equations. %This remarkable ability may stem from their capacity to model and generate multimodal distributions. In this work, we offer a novel perspective on the approach introduced in Song et al. (2021), shifting the focus from a "learning" problem to a "sampling" problem. To achieve this, we reformulate the equations governing diffusion-based generative models as a Forward-Backward Stochastic Differential Equation (FBSDE), which avoids the well-known issue of pre-estimating the gradient of the log target density. The solution of this FBSDE is proved to be unique using non-standard techniques. Additionally, we propose a numerical solution to this problem, leveraging on Deep Learning techniques. This reformulation opens new pathways for sampling multidimensional distributions with densities known up to a normalization constant, a problem frequently encountered in Bayesian statistics.

Statistical Learning and Inverse Problems: An Stochastic Gradient Approach

Inverse problems are paramount in Science and Engineering. In this paper, we consider the setup of Statistical Inverse Problem (SIP) and demonstrate how Stochastic Gradient Descent (SGD) algorithms can be used in the linear SIP setting. We provide consistency and finite sample bounds for the excess risk. We also propose a modification for the SGD algorithm where we leverage machine learning methods to smooth the stochastic gradients and improve empirical performance. We exemplify the algorithm in a setting of great interest nowadays: the Functional Linear Regression model. In this case we consider a synthetic data example and examples with a real data classification problem.

Functional Classification of Bitcoin Addresses

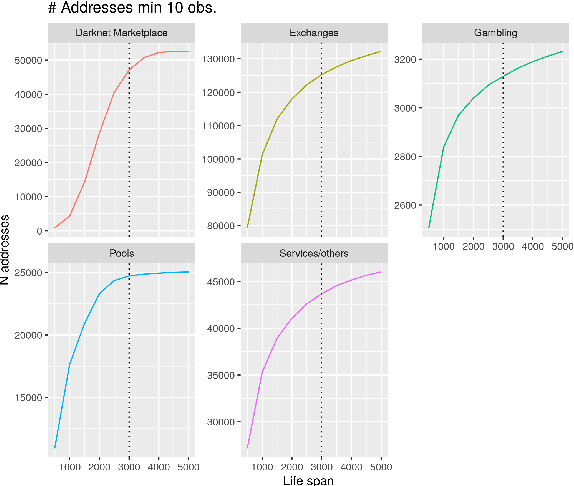
This paper proposes a classification model for predicting the main activity of bitcoin addresses based on their balances. Since the balances are functions of time, we apply methods from functional data analysis; more specifically, the features of the proposed classification model are the functional principal components of the data. Classifying bitcoin addresses is a relevant problem for two main reasons: to understand the composition of the bitcoin market, and to identify accounts used for illicit activities. Although other bitcoin classifiers have been proposed, they focus primarily on network analysis rather than curve behavior. Our approach, on the other hand, does not require any network information for prediction. Furthermore, functional features have the advantage of being straightforward to build, unlike expert-built features. Results show improvement when combining functional features with scalar features, and similar accuracy for the models using those features separately, which points to the functional model being a good alternative when domain-specific knowledge is not available.

PDGM: a Neural Network Approach to Solve Path-Dependent Partial Differential Equations

In this paper, we propose a novel numerical method for Path-Dependent Partial Differential Equations (PPDEs). These equations firstly appeared in the seminal work of Dupire [2009], where the functional It\^o calculus was developed to deal with path-dependent financial derivatives contracts. More specificaly, we generalize the Deep Galerking Method (DGM) of Sirignano and Spiliopoulos [2018] to deal with these equations. The method, which we call Path-Dependent DGM (PDGM), consists of using a combination of feed-forward and Long Short-Term Memory architectures to model the solution of the PPDE. We then analyze several numerical examples, many from the Financial Mathematics literature, that show the capabilities of the method under very different situations.