Yunseok Seo
Phase Diagram from Nonlinear Interaction between Superconducting Order and Density: Toward Data-Based Holographic Superconductor
Oct 09, 2024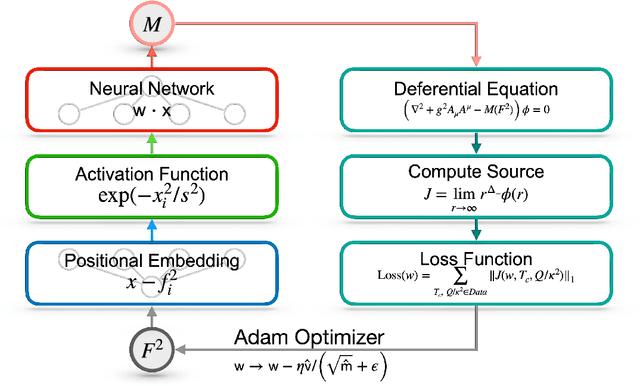
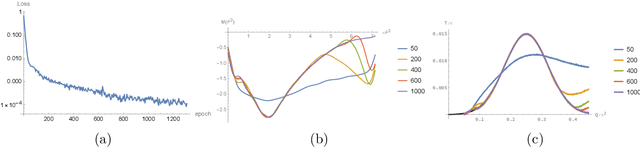
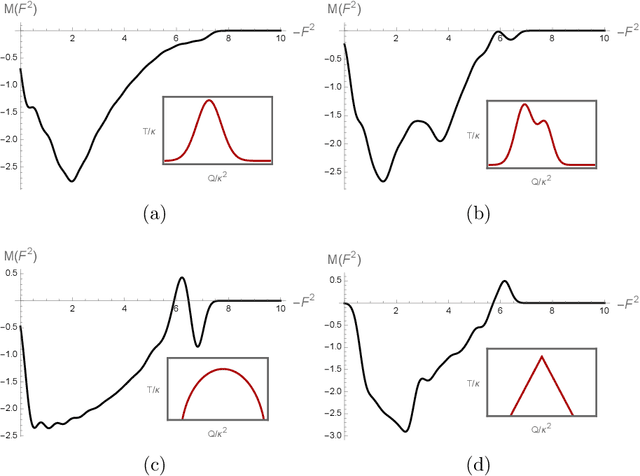
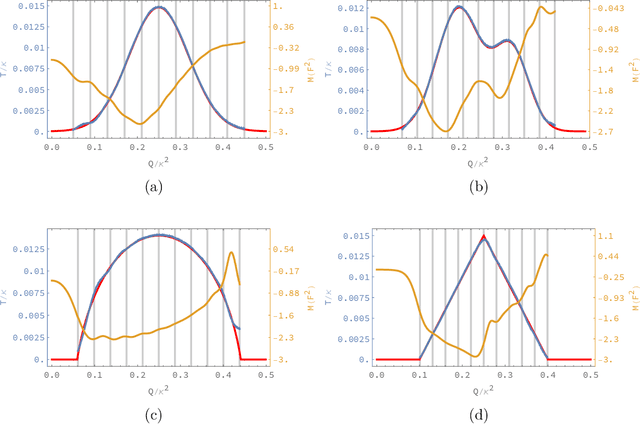
Abstract:We address an inverse problem in modeling holographic superconductors. We focus our research on the critical temperature behavior depicted by experiments. We use a physics-informed neural network method to find a mass function $M(F^2)$, which is necessary to understand phase transition behavior. This mass function describes a nonlinear interaction between superconducting order and charge carrier density. We introduce positional embedding layers to improve the learning process in our algorithm, and the Adam optimization is used to predict the critical temperature data via holographic calculation with appropriate accuracy. Consideration of the positional embedding layers is motivated by the transformer model of natural-language processing in the artificial intelligence (AI) field. We obtain holographic models that reproduce borderlines of the normal and superconducting phases provided by actual data. Our work is the first holographic attempt to match phase transition data quantitatively obtained from experiments. Also, the present work offers a new methodology for data-based holographic models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge