Revealing the evanescent components in Kronecker-product based codebooks: insights and implications

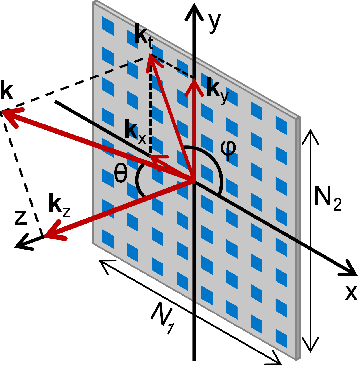
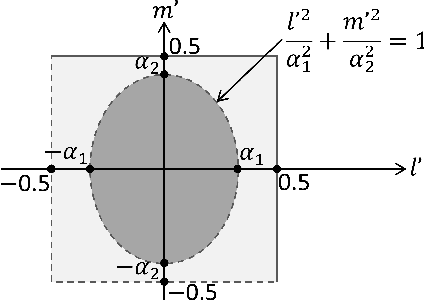
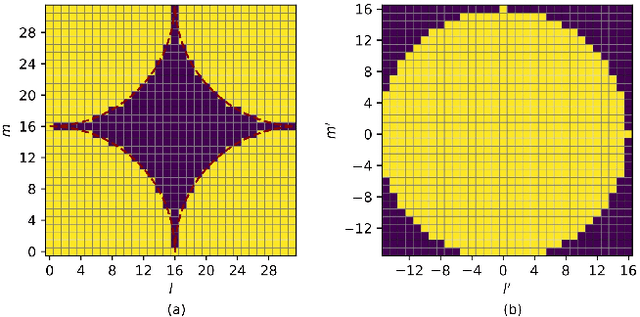
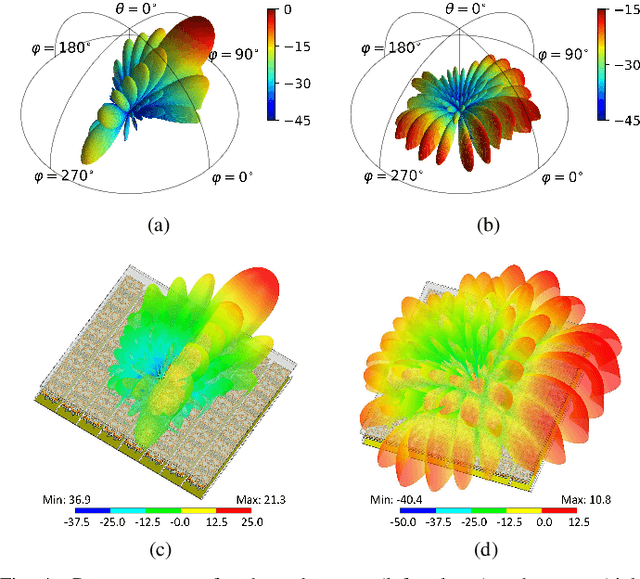
The orthogonal bases of discrete Fourier transform (DFT) has been recognized as the standard spatial-domain bases for Type I, Type II and enhanced Type II codewords by the 3rd Generation Partnership Project (3GPP). For uniform planar arrays, these spatial-domain bases are derived as the Kronecker product of one-dimensional DFT bases. Theoretically, each spatial basis corresponds to a beam directed towards a specific angle of departure and the set of bases represent the orthogonal beams that cover the front hemisphere of an array. While the Kronecker-product based precoding scheme facilitates the concise indexing of a codeword in the codebooks through precoding matrix indicators (PMIs) in channel state information feedback, it introduces redundant spatial beams characterized by high spatial-frequency components. This paper investigates the presence of codewords representing high spatial-frequency components within the Kronecker-product based codebooks. Through theoretical analysis and simulations, we confirm the redundancy of these codewords in MIMO communications, advocating for their removal from the codebooks to enhance system performance. Several topics relevant to the high spatial components are also involved in the discussion. Practical suggestions regarding future standard design are provided based on our theoretical analysis and simulation results.

Correction Algorithm of Sampling Effect and Its Application

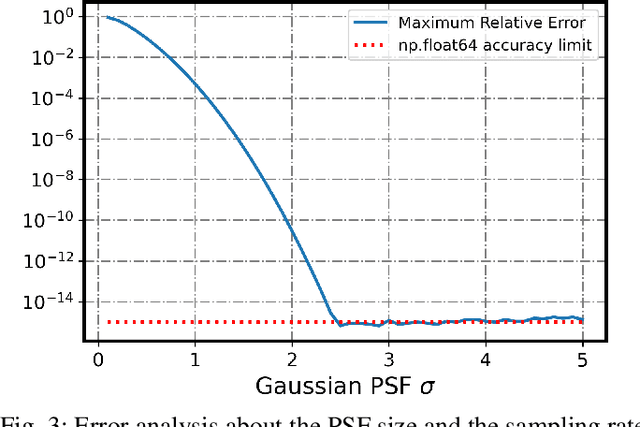
The sampling effect of the imaging acquisition device is long considered to be a modulation process of the input signal, introducing additional error into the signal acquisition process. This paper proposes a correction algorithm for the modulation process that solves the sampling effect with high accuracy. We examine the algorithm with perfect continuous Gaussian images and selected digitized images, which indicate an accuracy increase of 106 for Gaussian images, 102 at 15 times of Shannon interpolation for digitized images, and 105 at 101 times of Shannon interpolation for digitized images. The accuracy limit of the Gaussian image comes from the truncation error, while the accuracy limit of the digitized images comes from their finite resolution, which can be improved by increasing the time of Shannon interpolation.

Field Distortion Model Based on Fredholm Integral

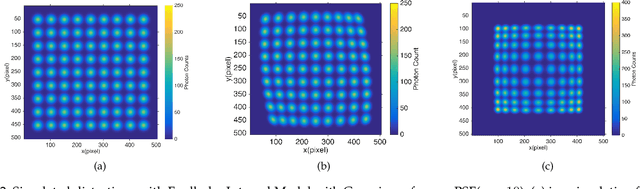
Field distortion is widespread in imaging systems. If it cannot be measured and corrected well, it will affect the accuracy of photogrammetry. To this end, we proposed a general field distortion model based on Fredholm integration, which uses a reconstructed high-resolution reference point spread function (PSF) and two sets of 4-variable polynomials to describe an imaging system. The model includes the point-to-point positional distortion from the object space to the image space and the deformation of the PSF so that we can measure an actual field distortion with arbitrary accuracy. We also derived the formula required for correcting the sampling effect of the image sensor. Through numerical simulation, we verify the effectiveness of the model and reconstruction algorithm. This model will have potential application in high-precision image calibration, photogrammetry and astrometry.