Movement-Specific Analysis for FIM Score Classification Using Spatio-Temporal Deep Learning

The functional independence measure (FIM) is widely used to evaluate patients' physical independence in activities of daily living. However, traditional FIM assessment imposes a significant burden on both patients and healthcare professionals. To address this challenge, we propose an automated FIM score estimation method that utilizes simple exercises different from the designated FIM assessment actions. Our approach employs a deep neural network architecture integrating a spatial-temporal graph convolutional network (ST-GCN), bidirectional long short-term memory (BiLSTM), and an attention mechanism to estimate FIM motor item scores. The model effectively captures long-term temporal dependencies and identifies key body-joint contributions through learned attention weights. We evaluated our method in a study of 277 rehabilitation patients, focusing on FIM transfer and locomotion items. Our approach successfully distinguishes between completely independent patients and those requiring assistance, achieving balanced accuracies of 70.09-78.79 % across different FIM items. Additionally, our analysis reveals specific movement patterns that serve as reliable predictors for particular FIM evaluation items.

A Recurrent Probabilistic Neural Network with Dimensionality Reduction Based on Time-series Discriminant Component Analysis

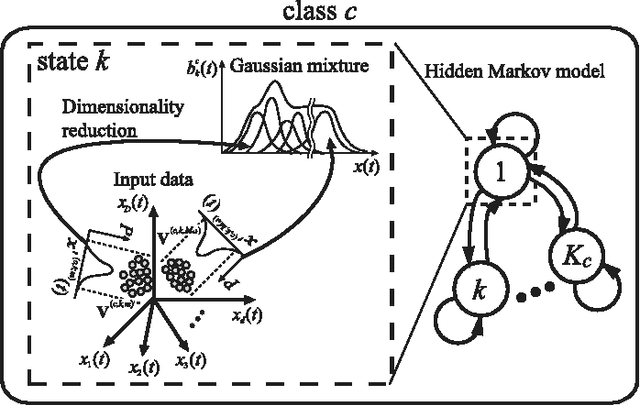
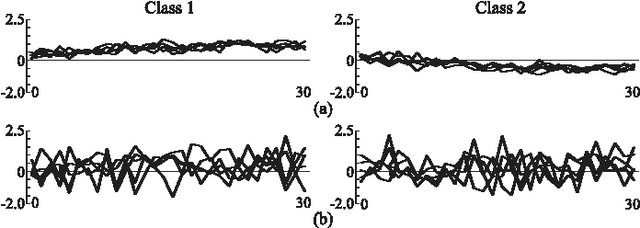
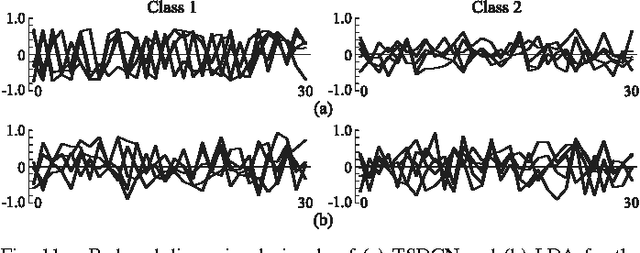
This paper proposes a probabilistic neural network developed on the basis of time-series discriminant component analysis (TSDCA) that can be used to classify high-dimensional time-series patterns. TSDCA involves the compression of high-dimensional time series into a lower-dimensional space using a set of orthogonal transformations and the calculation of posterior probabilities based on a continuous-density hidden Markov model with a Gaussian mixture model expressed in the reduced-dimensional space. The analysis can be incorporated into a neural network, which is named a time-series discriminant component network (TSDCN), so that parameters of dimensionality reduction and classification can be obtained simultaneously as network coefficients according to a backpropagation through time-based learning algorithm with the Lagrange multiplier method. The TSDCN is considered to enable high-accuracy classification of high-dimensional time-series patterns and to reduce the computation time taken for network training. The validity of the TSDCN is demonstrated for high-dimensional artificial data and EEG signals in the experiments conducted during the study.