Taro Shibanoki
A Neural Network Based on the Johnson $S_\mathrm{U}$ Translation System and Related Application to Electromyogram Classification
Nov 14, 2019


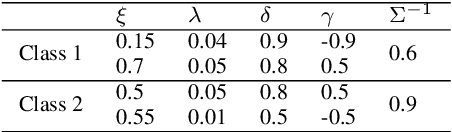
Abstract:Electromyogram (EMG) classification is a key technique in EMG-based control systems. The existing EMG classification methods do not consider the characteristics of EMG features that the distribution has skewness and kurtosis, causing drawbacks such as the requirement of hyperparameter tuning. In this paper, we propose a neural network based on the Johnson $S_\mathrm{U}$ translation system that is capable of representing distributions with skewness and kurtosis. The Johnson system is a normalizing translation that transforms non-normal data to a normal distribution, thereby enabling the representation of a wide range of distributions. In this study, a discriminative model based on the multivariate Johnson $S_\mathrm{U}$ translation system is transformed into a linear combination of coefficients and input vectors using log-linearization. This is then incorporated into a neural network structure, thereby allowing the calculation of the posterior probability of the input vectors for each class and the determination of model parameters as weight coefficients of the network. The uniqueness of convergence of the network learning is theoretically guaranteed. In the experiments, the suitability of the proposed network for distributions including skewness and kurtosis is evaluated using artificially generated data. Its applicability for real biological data is also evaluated via an EMG classification experiment. The results show that the proposed network achieves high classification performance without the need for hyperparameter optimization.
A Recurrent Probabilistic Neural Network with Dimensionality Reduction Based on Time-series Discriminant Component Analysis
Nov 14, 2019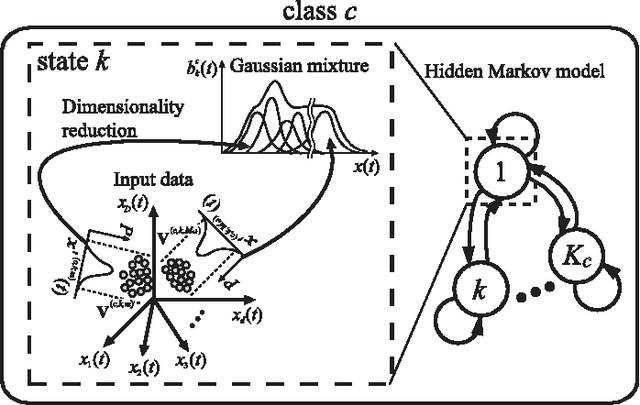

Abstract:This paper proposes a probabilistic neural network developed on the basis of time-series discriminant component analysis (TSDCA) that can be used to classify high-dimensional time-series patterns. TSDCA involves the compression of high-dimensional time series into a lower-dimensional space using a set of orthogonal transformations and the calculation of posterior probabilities based on a continuous-density hidden Markov model with a Gaussian mixture model expressed in the reduced-dimensional space. The analysis can be incorporated into a neural network, which is named a time-series discriminant component network (TSDCN), so that parameters of dimensionality reduction and classification can be obtained simultaneously as network coefficients according to a backpropagation through time-based learning algorithm with the Lagrange multiplier method. The TSDCN is considered to enable high-accuracy classification of high-dimensional time-series patterns and to reduce the computation time taken for network training. The validity of the TSDCN is demonstrated for high-dimensional artificial data and EEG signals in the experiments conducted during the study.
* Published in IEEE Transactions on Neural Networks and Learning Systems
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge