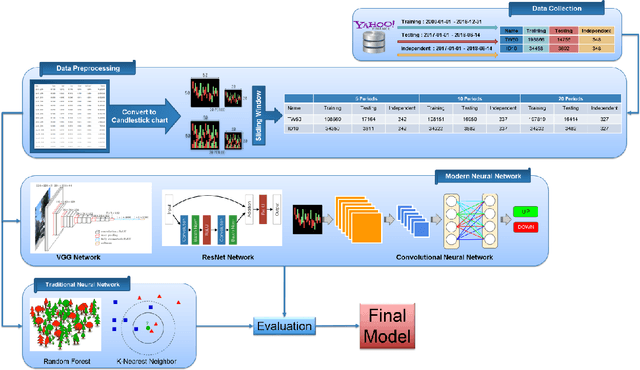
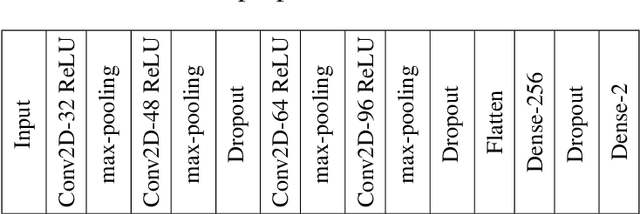
Using Deep Learning Neural Networks and Candlestick Chart Representation to Predict Stock Market

Stock market prediction is still a challenging problem because there are many factors effect to the stock market price such as company news and performance, industry performance, investor sentiment, social media sentiment and economic factors. This work explores the predictability in the stock market using Deep Convolutional Network and candlestick charts. The outcome is utilized to design a decision support framework that can be used by traders to provide suggested indications of future stock price direction. We perform this work using various types of neural networks like convolutional neural network, residual network and visual geometry group network. From stock market historical data, we converted it to candlestick charts. Finally, these candlestick charts will be feed as input for training a Convolutional Neural Network model. This Convolutional Neural Network model will help us to analyze the patterns inside the candlestick chart and predict the future movements of stock market. The effectiveness of our method is evaluated in stock market prediction with a promising results 92.2% and 92.1% accuracy for Taiwan and Indonesian stock market dataset respectively. The constructed model have been implemented as a web-based system freely available at http://140.138.155.216/deepcandle/ for predicting stock market using candlestick chart and deep learning neural networks.

Supervised Machine Learning with a Novel Kernel Density Estimator

In recent years, kernel density estimation has been exploited by computer scientists to model machine learning problems. The kernel density estimation based approaches are of interest due to the low time complexity of either O(n) or O(n*log(n)) for constructing a classifier, where n is the number of sampling instances. Concerning design of kernel density estimators, one essential issue is how fast the pointwise mean square error (MSE) and/or the integrated mean square error (IMSE) diminish as the number of sampling instances increases. In this article, it is shown that with the proposed kernel function it is feasible to make the pointwise MSE of the density estimator converge at O(n^-2/3) regardless of the dimension of the vector space, provided that the probability density function at the point of interest meets certain conditions.