Interpretability for Conditional Coordinated Behavior in Multi-Agent Reinforcement Learning

We propose a model-free reinforcement learning architecture, called distributed attentional actor architecture after conditional attention (DA6-X), to provide better interpretability of conditional coordinated behaviors. The underlying principle involves reusing the saliency vector, which represents the conditional states of the environment, such as the global position of agents. Hence, agents with DA6-X flexibility built into their policy exhibit superior performance by considering the additional information in the conditional states during the decision-making process. The effectiveness of the proposed method was experimentally evaluated by comparing it with conventional methods in an objects collection game. By visualizing the attention weights from DA6-X, we confirmed that agents successfully learn situation-dependent coordinated behaviors by correctly identifying various conditional states, leading to improved interpretability of agents along with superior performance.

Distributed Multi-Agent Deep Reinforcement Learning for Robust Coordination against Noise

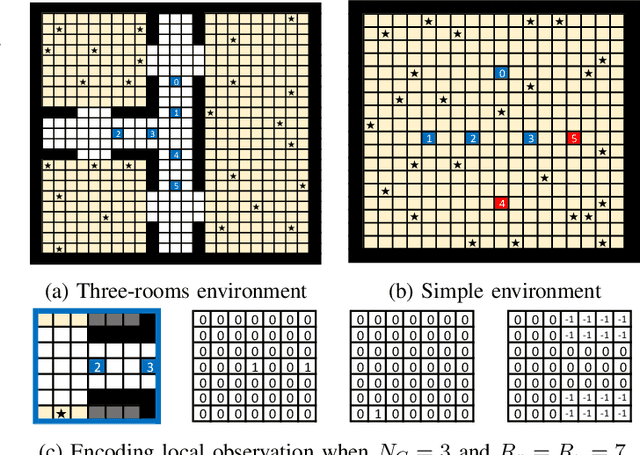
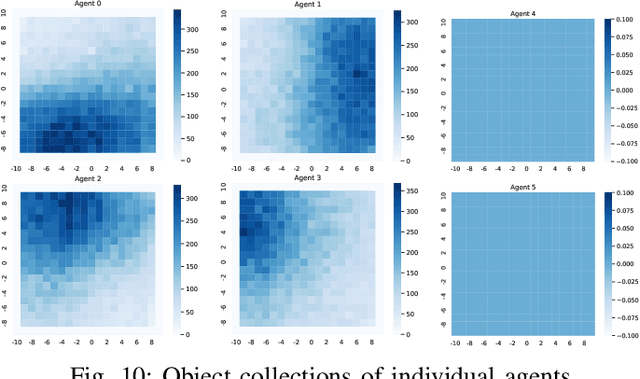
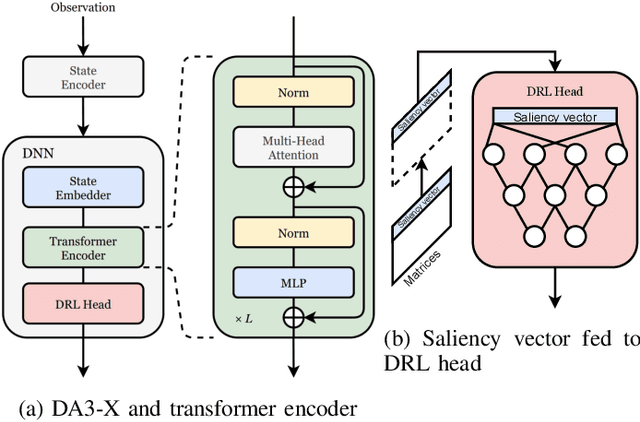
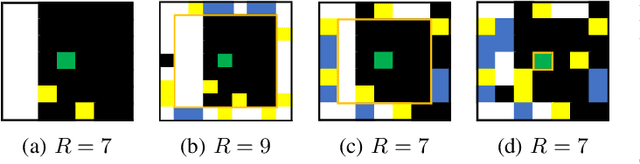
In multi-agent systems, noise reduction techniques are important for improving the overall system reliability as agents are required to rely on limited environmental information to develop cooperative and coordinated behaviors with the surrounding agents. However, previous studies have often applied centralized noise reduction methods to build robust and versatile coordination in noisy multi-agent environments, while distributed and decentralized autonomous agents are more plausible for real-world application. In this paper, we introduce a \emph{distributed attentional actor architecture model for a multi-agent system} (DA3-X), using which we demonstrate that agents with DA3-X can selectively learn the noisy environment and behave cooperatively. We experimentally evaluate the effectiveness of DA3-X by comparing learning methods with and without DA3-X and show that agents with DA3-X can achieve better performance than baseline agents. Furthermore, we visualize heatmaps of \emph{attentional weights} from the DA3-X to analyze how the decision-making process and coordinated behavior are influenced by noise.