Regression for matrix-valued data via Kronecker products factorization

We study the matrix-variate regression problem $Y_i = \sum_{k} \beta_{1k} X_i \beta_{2k}^{\top} + E_i$ for $i=1,2\dots,n$ in the high dimensional regime wherein the response $Y_i$ are matrices whose dimensions $p_{1}\times p_{2}$ outgrow both the sample size $n$ and the dimensions $q_{1}\times q_{2}$ of the predictor variables $X_i$ i.e., $q_{1},q_{2} \ll n \ll p_{1},p_{2}$. We propose an estimation algorithm, termed KRO-PRO-FAC, for estimating the parameters $\{\beta_{1k}\} \subset \Re^{p_1 \times q_1}$ and $\{\beta_{2k}\} \subset \Re^{p_2 \times q_2}$ that utilizes the Kronecker product factorization and rearrangement operations from Van Loan and Pitsianis (1993). The KRO-PRO-FAC algorithm is computationally efficient as it does not require estimating the covariance between the entries of the $\{Y_i\}$. We establish perturbation bounds between $\hat{\beta}_{1k} -\beta_{1k}$ and $\hat{\beta}_{2k} - \beta_{2k}$ in spectral norm for the setting where either the rows of $E_i$ or the columns of $E_i$ are independent sub-Gaussian random vectors. Numerical studies on simulated and real data indicate that our procedure is competitive, in terms of both estimation error and predictive accuracy, compared to other existing methods.

Classification of high-dimensional data with spiked covariance matrix structure

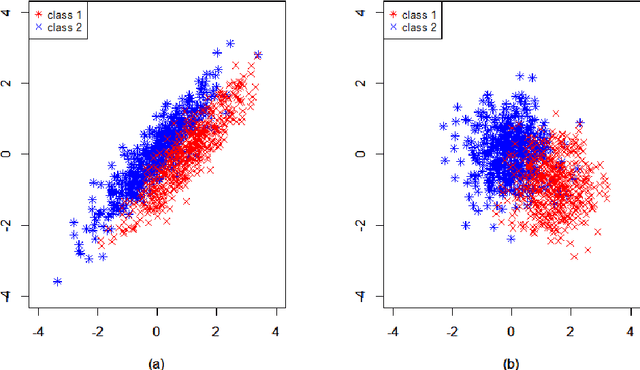
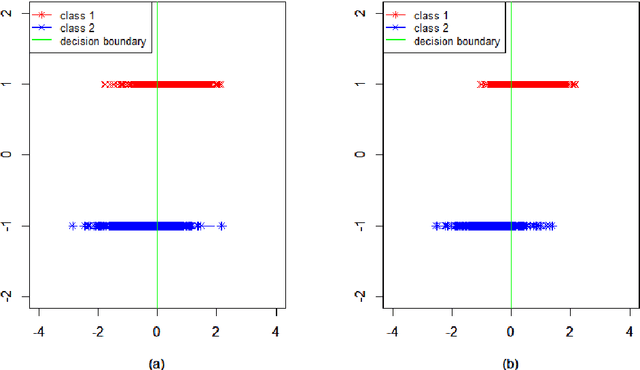
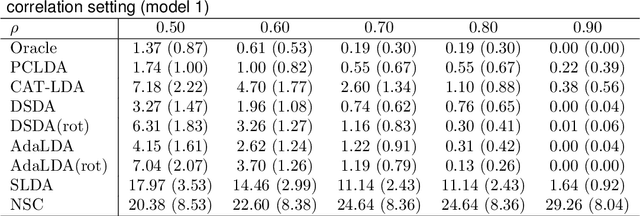
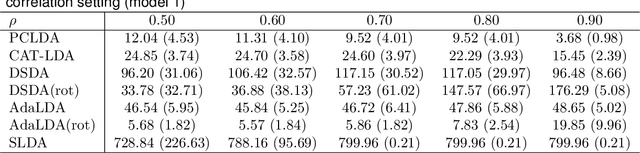
We study the classification problem for high-dimensional data with $n$ observations on $p$ features where the $p \times p$ covariance matrix $\Sigma$ exhibits a spiked eigenvalues structure and the vector $\zeta$, given by the difference between the whitened mean vectors, is sparse with sparsity at most $s$. We propose an adaptive classifier (adaptive with respect to the sparsity $s$) that first performs dimension reduction on the feature vectors prior to classification in the dimensionally reduced space, i.e., the classifier whitened the data, then screen the features by keeping only those corresponding to the $s$ largest coordinates of $\zeta$ and finally apply Fisher linear discriminant on the selected features. Leveraging recent results on entrywise matrix perturbation bounds for covariance matrices, we show that the resulting classifier is Bayes optimal whenever $n \rightarrow \infty$ and $s \sqrt{n^{-1} \ln p} \rightarrow 0$. Experimental results on real and synthetic data sets indicate that the proposed classifier is competitive with existing state-of-the-art methods while also selecting a smaller number of features.