Classification of high-dimensional data with spiked covariance matrix structure
Paper and Code
Oct 05, 2021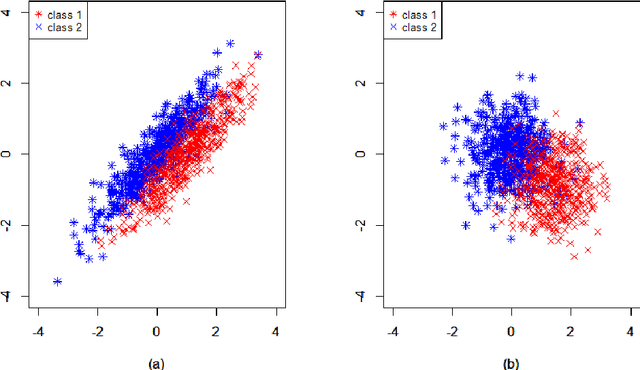
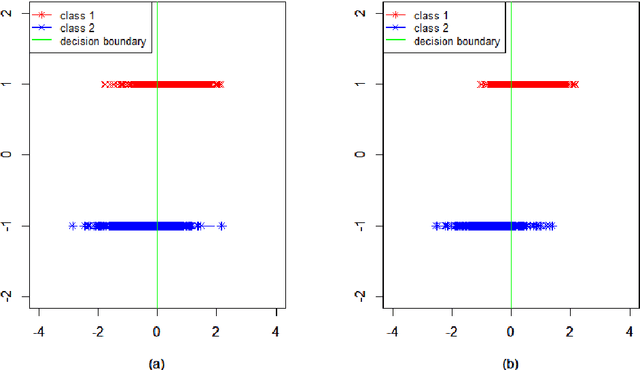
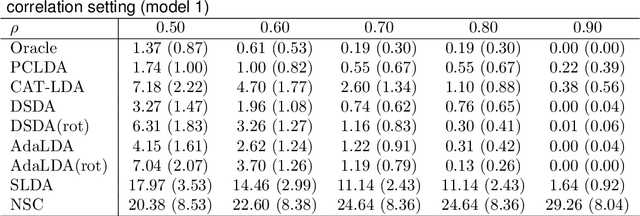
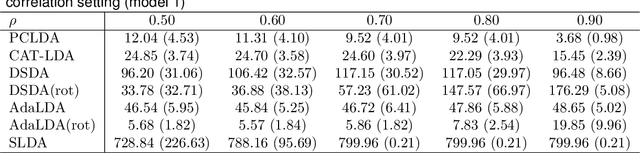
We study the classification problem for high-dimensional data with $n$ observations on $p$ features where the $p \times p$ covariance matrix $\Sigma$ exhibits a spiked eigenvalues structure and the vector $\zeta$, given by the difference between the whitened mean vectors, is sparse with sparsity at most $s$. We propose an adaptive classifier (adaptive with respect to the sparsity $s$) that first performs dimension reduction on the feature vectors prior to classification in the dimensionally reduced space, i.e., the classifier whitened the data, then screen the features by keeping only those corresponding to the $s$ largest coordinates of $\zeta$ and finally apply Fisher linear discriminant on the selected features. Leveraging recent results on entrywise matrix perturbation bounds for covariance matrices, we show that the resulting classifier is Bayes optimal whenever $n \rightarrow \infty$ and $s \sqrt{n^{-1} \ln p} \rightarrow 0$. Experimental results on real and synthetic data sets indicate that the proposed classifier is competitive with existing state-of-the-art methods while also selecting a smaller number of features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge