Yilin Xia
On the Structure of Game Provenance and its Applications
Oct 07, 2024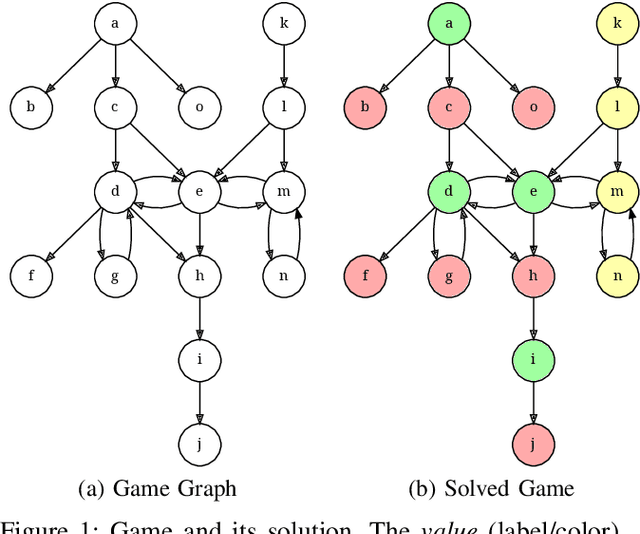
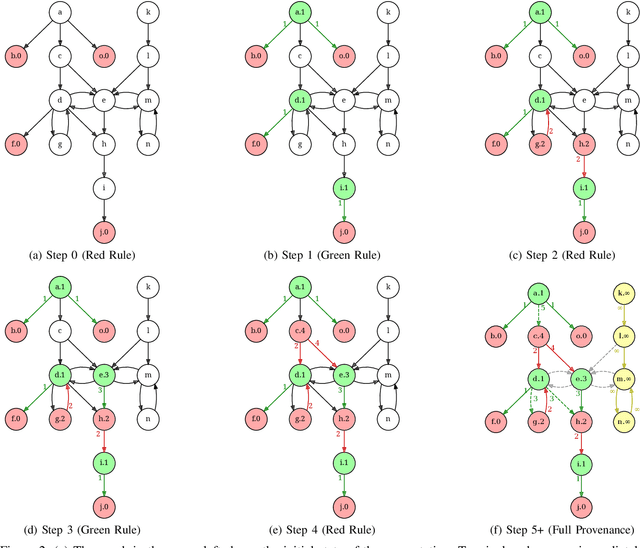
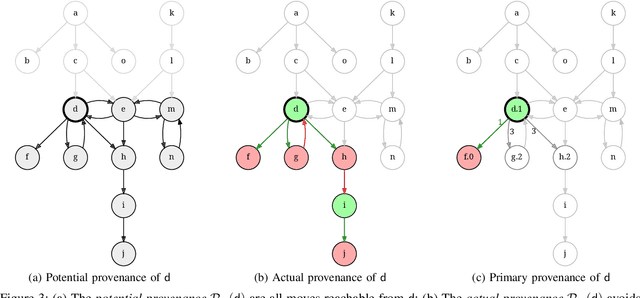
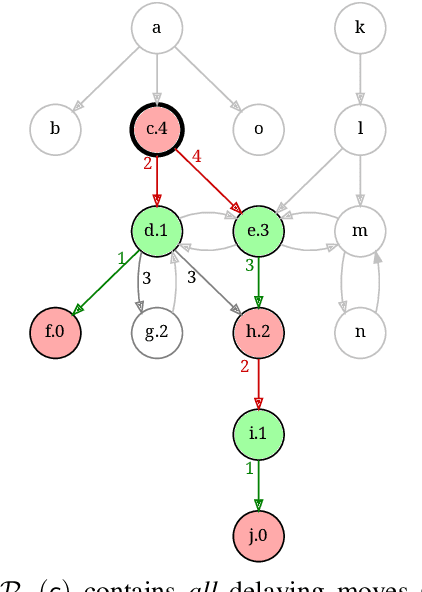
Abstract:Provenance in databases has been thoroughly studied for positive and for recursive queries, then for first-order (FO) queries, i.e., having negation but no recursion. Query evaluation can be understood as a two-player game where the opponents argue whether or not a tuple is in the query answer. This game-theoretic approach yields a natural provenance model for FO queries, unifying how and why-not provenance. Here, we study the fine-grain structure of game provenance. A game $G=(V,E)$ consists of positions $V$ and moves $E$ and can be solved by computing the well-founded model of a single, unstratifiable rule: \[ \text{win}(X) \leftarrow \text{move}(X, Y), \neg \, \text{win}(Y). \] In the solved game $G^{\lambda}$, the value of a position $x\,{\in}\,V$ is either won, lost, or drawn. This value is explained by the provenance $\mathscr{P}$(x), i.e., certain (annotated) edges reachable from $x$. We identify seven edge types that give rise to new kinds of provenance, i.e., potential, actual, and primary, and demonstrate that "not all moves are created equal". We describe the new provenance types, show how they can be computed while solving games, and discuss applications, e.g., for abstract argumentation frameworks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge