Yayu Yao
UCB-driven Utility Function Search for Multi-objective Reinforcement Learning
May 01, 2024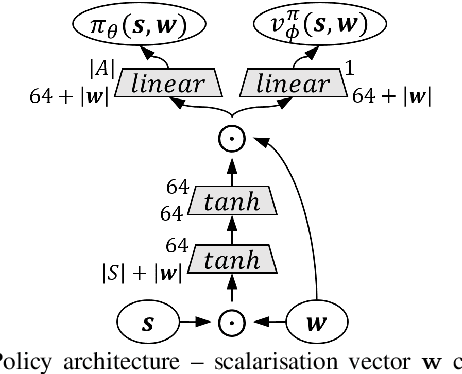
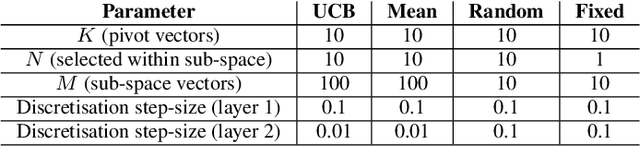
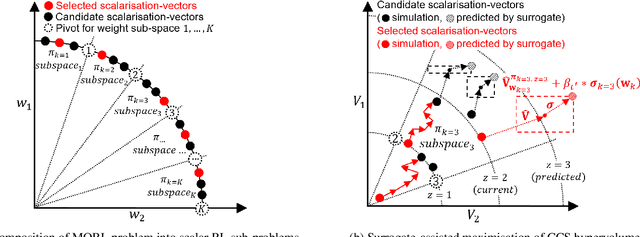
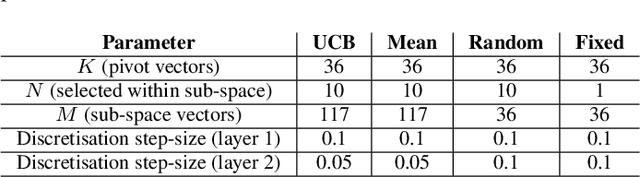
Abstract:In Multi-objective Reinforcement Learning (MORL) agents are tasked with optimising decision-making behaviours that trade-off between multiple, possibly conflicting, objectives. MORL based on decomposition is a family of solution methods that employ a number of utility functions to decompose the multi-objective problem into individual single-objective problems solved simultaneously in order to approximate a Pareto front of policies. We focus on the case of linear utility functions parameterised by weight vectors w. We introduce a method based on Upper Confidence Bound to efficiently search for the most promising weight vectors during different stages of the learning process, with the aim of maximising the hypervolume of the resulting Pareto front. The proposed method is shown to outperform various MORL baselines on Mujoco benchmark problems across different random seeds. The code is online at: https://github.com/SYCAMORE-1/ucb-MOPPO.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge