Low PAPR MIMO-OFDM Design Based on Convolutional Autoencoder

An enhanced framework for peak-to-average power ratio ($\mathsf{PAPR}$) reduction and waveform design for Multiple-Input-Multiple-Output ($\mathsf{MIMO}$) orthogonal frequency-division multiplexing ($\mathsf{OFDM}$) systems, based on a convolutional-autoencoder ($\mathsf{CAE}$) architecture, is presented. The end-to-end learning-based autoencoder ($\mathsf{AE}$) for communication networks represents the network by an encoder and decoder, where in between, the learned latent representation goes through a physical communication channel. We introduce a joint learning scheme based on projected gradient descent iteration to optimize the spectral mask behavior and MIMO detection under the influence of a non-linear high power amplifier ($\mathsf{HPA}$) and a multipath fading channel. The offered efficient implementation novel waveform design technique utilizes only a single $\mathsf{PAPR}$ reduction block for all antennas. It is throughput-lossless, as no side information is required at the decoder. Performance is analyzed by examining the bit error rate ($\mathsf{BER}$), the $\mathsf{PAPR}$, and the spectral response and compared with classical $\mathsf{PAPR}$ reduction $\mathsf{MIMO}$ detector methods on 5G simulated data. The suggested system exhibits competitive performance when considering all optimization criteria simultaneously. We apply gradual loss learning for multi-objective optimization and show empirically that a single trained model covers the tasks of $\mathsf{PAPR}$ reduction, spectrum design, and $\mathsf{MIMO}$ detection together over a wide range of SNR levels.

Low PAPR waveform design for OFDM SYSTEM based on Convolutional Auto-Encoder

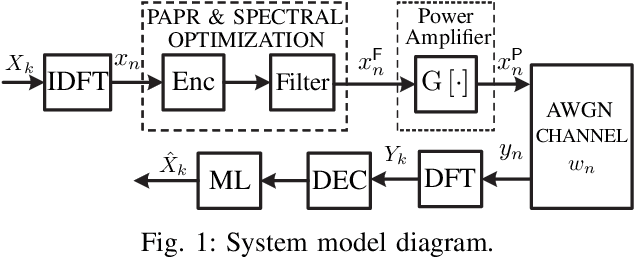
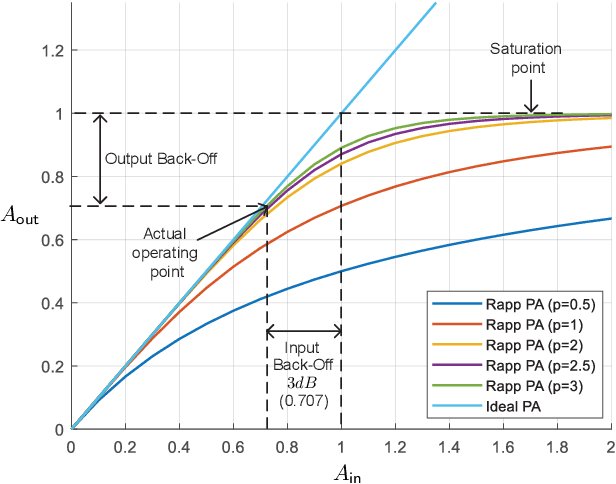
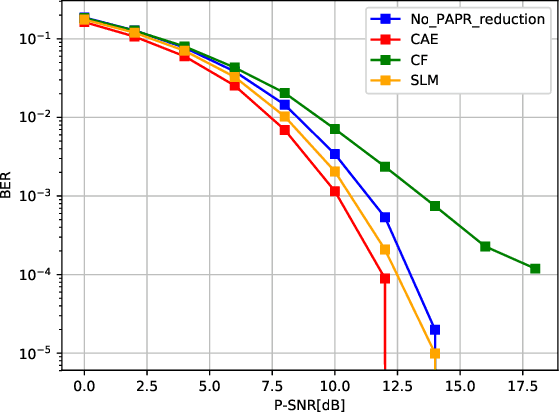
This paper introduces the architecture of a convolutional autoencoder (CAE) for the task of peak-to-average power ratio (PAPR) reduction and waveform design, for orthogonal frequency division multiplexing (OFDM) systems. The proposed architecture integrates a PAPR reduction block and a non-linear high power amplifier (HPA) model. We apply gradual loss learning for multi-objective optimization. We analyze the models performance by examining the bit error rate (BER), the PAPR and the spectral response, and comparing them with common PAPR reduction algorithms.