A swarm intelligence-based robust solution for Virtual Reference Feedback Tuning

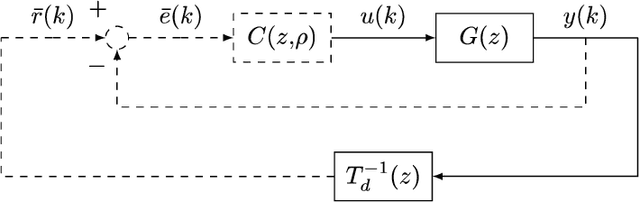
This work proposes the inclusion of an $\mathcal{H}_{\infty}$ robustness constraint to the Virtual Reference Feedback Tuning (VRFT) cost function, which is solved by metaheuristic optimization with only a single batch of data (one-shot). The $\mathcal{H}_{\infty}$ norm of the sensitivity function is estimated in a data-driven fashion, based on the regularized estimation of the system's impulse response. Four different swarm intelligence algorithms are chosen to be evaluated and compared at the optimization problem. Two real-world based examples are used to illustrate the proposed method through a Monte Carlo experiment with 50 runs. To compare the swarm intelligence algorithms to each other, 50 search agents have been adopted, with a maximum number of iterations of 100. For all cases, the Improved Grey Wolf Optimizer (I-GWO) algorithm presented the least number of outliers and faster convergence, with the closest dynamic behavior to the desired, satisfying the imposed robustness constraint with lower fitness than other tested algorithms.

Data-driven estimation of system norms via impulse response

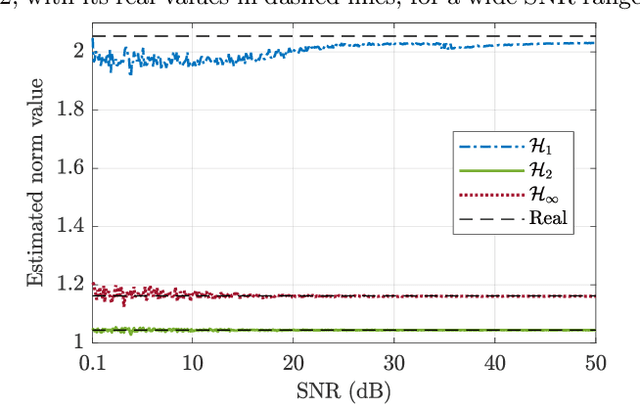
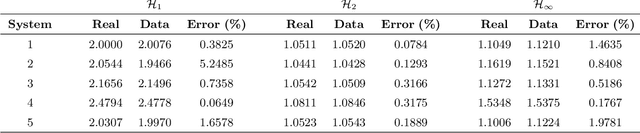
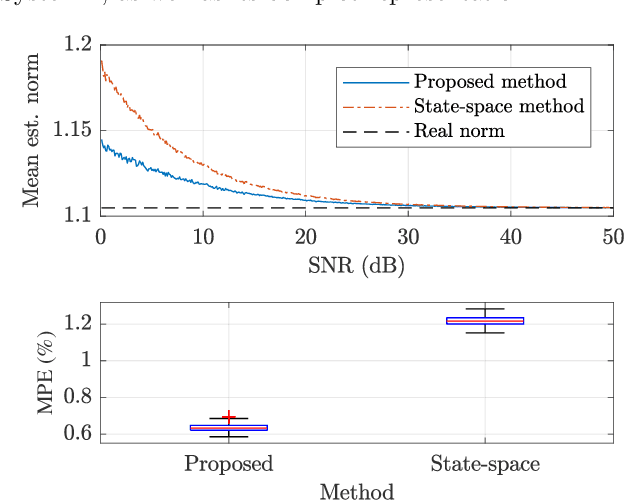
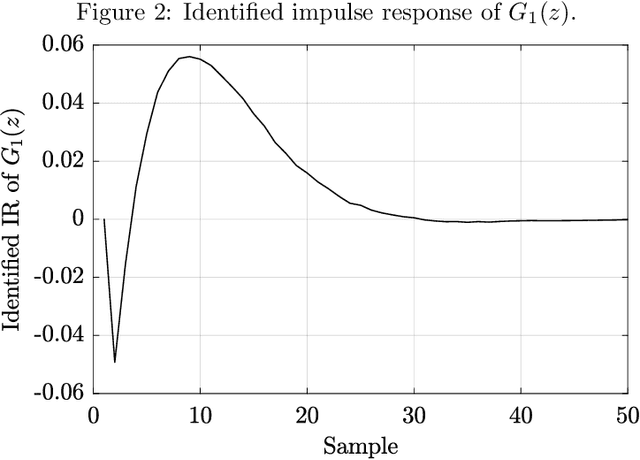
This paper proposes a method for estimating the norms of a system in a pure data-driven fashion based on their identified Impulse Response (IR) coefficients. The calculation of norms is briefly reviewed and the main expressions for the IR-based estimations are presented. As a case study, the $\mathcal{H}_{1}$, $\mathcal{H}_2$, and $\mathcal{H}_{\infty}$ norms of the sensitivity transfer function of five different discrete-time closed-loop systems are estimated for a Signal-to-Noise-Ratio (SNR) of 10 dB, achieving low percent error values if compared to the real value. To verify the influence of the noise amplitude, norms are estimated considering a wide range of SNR values, for a specific system, presenting low Mean Percent Error (MPE) if compared to the real norms. The proposed technique is also compared to an existing state-space-based method in terms of $\mathcal{H}_{\infty}$, through Monte Carlo, showing a reduction of approximately 48 % in the MPE for a wide range of SNR values.