Data-driven estimation of system norms via impulse response
Paper and Code
Nov 08, 2021
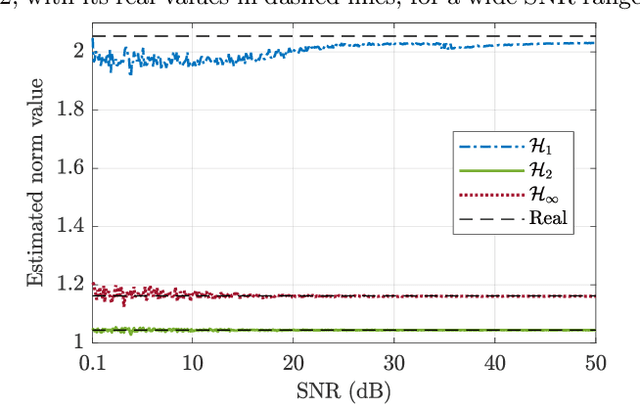
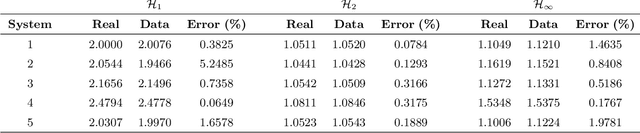
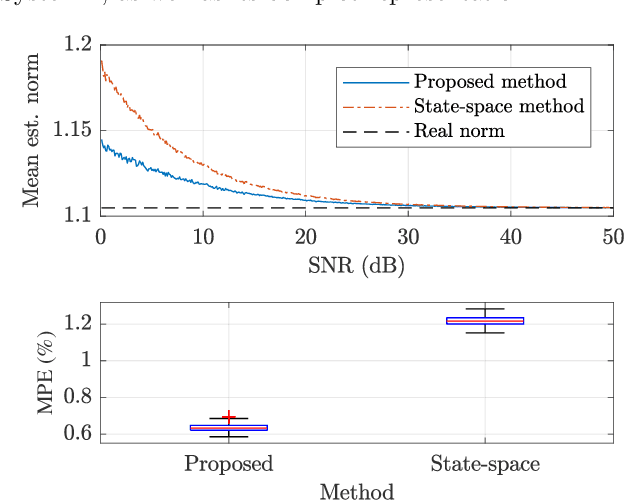
This paper proposes a method for estimating the norms of a system in a pure data-driven fashion based on their identified Impulse Response (IR) coefficients. The calculation of norms is briefly reviewed and the main expressions for the IR-based estimations are presented. As a case study, the $\mathcal{H}_{1}$, $\mathcal{H}_2$, and $\mathcal{H}_{\infty}$ norms of the sensitivity transfer function of five different discrete-time closed-loop systems are estimated for a Signal-to-Noise-Ratio (SNR) of 10 dB, achieving low percent error values if compared to the real value. To verify the influence of the noise amplitude, norms are estimated considering a wide range of SNR values, for a specific system, presenting low Mean Percent Error (MPE) if compared to the real norms. The proposed technique is also compared to an existing state-space-based method in terms of $\mathcal{H}_{\infty}$, through Monte Carlo, showing a reduction of approximately 48 % in the MPE for a wide range of SNR values.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge