Parameter-Adaptive Dynamic Pricing

Dynamic pricing is crucial in sectors like e-commerce and transportation, balancing exploration of demand patterns and exploitation of pricing strategies. Existing methods often require precise knowledge of the demand function, e.g., the H{\"o}lder smoothness level and Lipschitz constant, limiting practical utility. This paper introduces an adaptive approach to address these challenges without prior parameter knowledge. By partitioning the demand function's domain and employing a linear bandit structure, we develop an algorithm that manages regret efficiently, enhancing flexibility and practicality. Our Parameter-Adaptive Dynamic Pricing (PADP) algorithm outperforms existing methods, offering improved regret bounds and extensions for contextual information. Numerical experiments validate our approach, demonstrating its superiority in handling unknown demand parameters.

Minimax Optimality in Contextual Dynamic Pricing with General Valuation Models

Dynamic pricing, the practice of adjusting prices based on contextual factors, has gained significant attention due to its impact on revenue maximization. In this paper, we address the contextual dynamic pricing problem, which involves pricing decisions based on observable product features and customer characteristics. We propose a novel algorithm that achieves improved regret bounds while minimizing assumptions about the problem. Our algorithm discretizes the unknown noise distribution and combines the upper confidence bounds with a layered data partitioning technique to effectively regulate regret in each episode. These techniques effectively control the regret associated with pricing decisions, leading to the minimax optimality. Specifically, our algorithm achieves a regret upper bound of $\tilde{\mathcal{O}}(\rho_{\mathcal{V}}^{\frac{1}{3}}(\delta) T^{\frac{2}{3}})$, where $\rho_{\mathcal{V}}(\delta)$ represents the estimation error of the valuation function. Importantly, this bound matches the lower bound up to logarithmic terms, demonstrating the minimax optimality of our approach. Furthermore, our method extends beyond linear valuation models commonly used in dynamic pricing by considering general function spaces. We simplify the estimation process by reducing it to general offline regression oracles, making implementation more straightforward.

Stochastic Graph Bandit Learning with Side-Observations

In this paper, we investigate the stochastic contextual bandit with general function space and graph feedback. We propose an algorithm that addresses this problem by adapting to both the underlying graph structures and reward gaps. To the best of our knowledge, our algorithm is the first to provide a gap-dependent upper bound in this stochastic setting, bridging the research gap left by the work in [35]. In comparison to [31,33,35], our method offers improved regret upper bounds and does not require knowledge of graphical quantities. We conduct numerical experiments to demonstrate the computational efficiency and effectiveness of our approach in terms of regret upper bounds. These findings highlight the significance of our algorithm in advancing the field of stochastic contextual bandits with graph feedback, opening up avenues for practical applications in various domains.

Provably Efficient Learning in Partially Observable Contextual Bandit

In this paper, we investigate transfer learning in partially observable contextual bandits, where agents have limited knowledge from other agents and partial information about hidden confounders. We first convert the problem to identifying or partially identifying causal effects between actions and rewards through optimization problems. To solve these optimization problems, we discretize the original functional constraints of unknown distributions into linear constraints, and sample compatible causal models via sequentially solving linear programmings to obtain causal bounds with the consideration of estimation error. Our sampling algorithms provide desirable convergence results for suitable sampling distributions. We then show how causal bounds can be applied to improving classical bandit algorithms and affect the regrets with respect to the size of action sets and function spaces. Notably, in the task with function approximation which allows us to handle general context distributions, our method improves the order dependence on function space size compared with previous literatures. We formally prove that our causally enhanced algorithms outperform classical bandit algorithms and achieve orders of magnitude faster convergence rates. Finally, we perform simulations that demonstrate the efficiency of our strategy compared to the current state-of-the-art methods. This research has the potential to enhance the performance of contextual bandit agents in real-world applications where data is scarce and costly to obtain.

Dual Instrumental Method for Confounded Kernelized Bandits

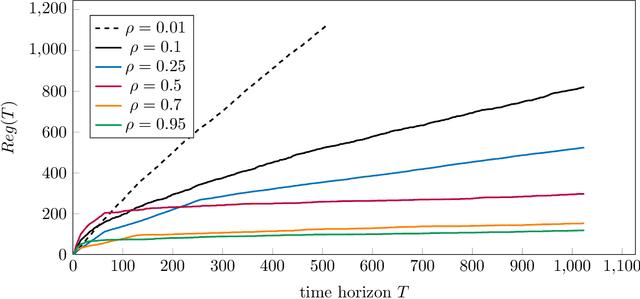
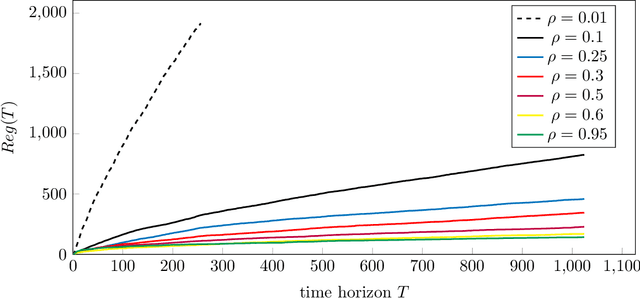
The contextual bandit problem is a theoretically justified framework with wide applications in various fields. While the previous study on this problem usually requires independence between noise and contexts, our work considers a more sensible setting where the noise becomes a latent confounder that affects both contexts and rewards. Such a confounded setting is more realistic and could expand to a broader range of applications. However, the unresolved confounder will cause a bias in reward function estimation and thus lead to a large regret. To deal with the challenges brought by the confounder, we apply the dual instrumental variable regression, which can correctly identify the true reward function. We prove the convergence rate of this method is near-optimal in two types of widely used reproducing kernel Hilbert spaces. Therefore, we can design computationally efficient and regret-optimal algorithms based on the theoretical guarantees for confounded bandit problems. The numerical results illustrate the efficacy of our proposed algorithms in the confounded bandit setting.