Dual Instrumental Method for Confounded Kernelized Bandits
Paper and Code
Sep 07, 2022

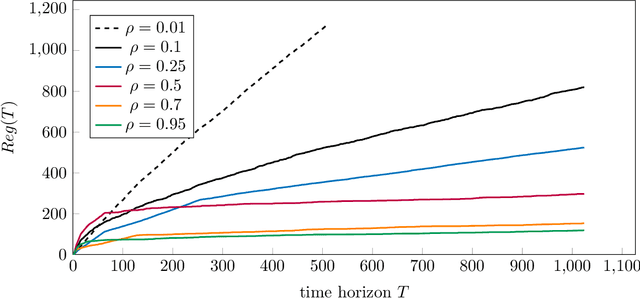
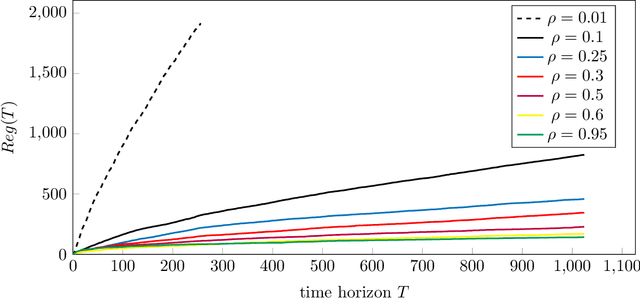
The contextual bandit problem is a theoretically justified framework with wide applications in various fields. While the previous study on this problem usually requires independence between noise and contexts, our work considers a more sensible setting where the noise becomes a latent confounder that affects both contexts and rewards. Such a confounded setting is more realistic and could expand to a broader range of applications. However, the unresolved confounder will cause a bias in reward function estimation and thus lead to a large regret. To deal with the challenges brought by the confounder, we apply the dual instrumental variable regression, which can correctly identify the true reward function. We prove the convergence rate of this method is near-optimal in two types of widely used reproducing kernel Hilbert spaces. Therefore, we can design computationally efficient and regret-optimal algorithms based on the theoretical guarantees for confounded bandit problems. The numerical results illustrate the efficacy of our proposed algorithms in the confounded bandit setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge