Cross-Fusion Distance: A Novel Metric for Measuring Fusion and Separability Between Data Groups in Representation Space

Quantifying degrees of fusion and separability between data groups in representation space is a fundamental problem in representation learning, particularly under domain shift. A meaningful metric should capture fusion-altering factors like geometric displacement between representation groups, whose variations change the extent of fusion, while remaining invariant to fusion-preserving factors such as global scaling and sampling-induced layout changes, whose variations do not. Existing distributional distance metrics conflate these factors, leading to measures that are not informative of the true extent of fusion between data groups. We introduce Cross-Fusion Distance (CFD), a principled measure that isolates fusion-altering geometry while remaining robust to fusion-preserving variations, with linear computational complexity. We characterize the invariance and sensitivity properties of CFD theoretically and validate them in controlled synthetic experiments. For practical utility on real-world datasets with domain shift, CFD aligns more closely with downstream generalization degradation than commonly used alternatives. Overall, CFD provides a theoretically grounded and interpretable distance measure for representation learning.

Data Valuation with Gradient Similarity

High-quality data is crucial for accurate machine learning and actionable analytics, however, mislabeled or noisy data is a common problem in many domains. Distinguishing low- from high-quality data can be challenging, often requiring expert knowledge and considerable manual intervention. Data Valuation algorithms are a class of methods that seek to quantify the value of each sample in a dataset based on its contribution or importance to a given predictive task. These data values have shown an impressive ability to identify mislabeled observations, and filtering low-value data can boost machine learning performance. In this work, we present a simple alternative to existing methods, termed Data Valuation with Gradient Similarity (DVGS). This approach can be easily applied to any gradient descent learning algorithm, scales well to large datasets, and performs comparably or better than baseline valuation methods for tasks such as corrupted label discovery and noise quantification. We evaluate the DVGS method on tabular, image and RNA expression datasets to show the effectiveness of the method across domains. Our approach has the ability to rapidly and accurately identify low-quality data, which can reduce the need for expert knowledge and manual intervention in data cleaning tasks.

Efficient Self-Ensemble Framework for Semantic Segmentation

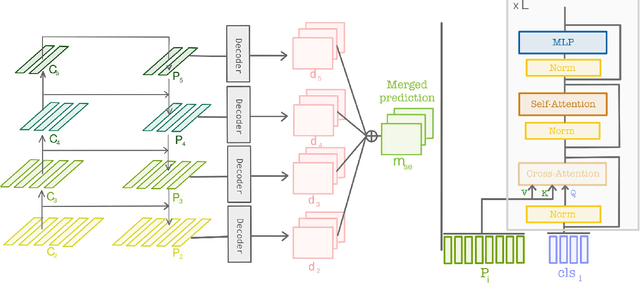
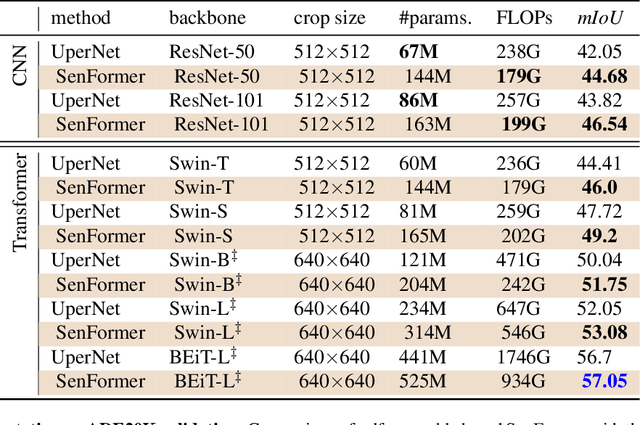
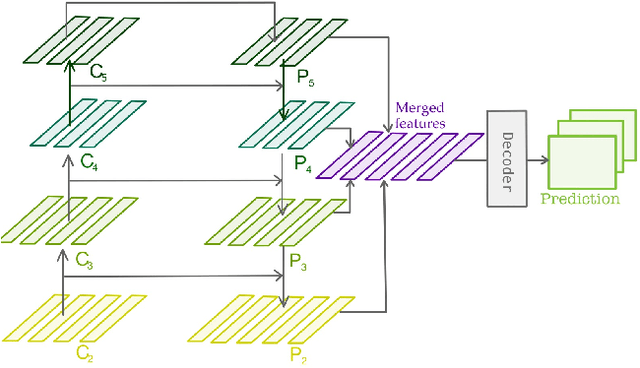
Ensemble of predictions is known to perform better than individual predictions taken separately. However, for tasks that require heavy computational resources, \textit{e.g.} semantic segmentation, creating an ensemble of learners that needs to be trained separately is hardly tractable. In this work, we propose to leverage the performance boost offered by ensemble methods to enhance the semantic segmentation, while avoiding the traditional heavy training cost of the ensemble. Our self-ensemble framework takes advantage of the multi-scale features set produced by feature pyramid network methods to feed independent decoders, thus creating an ensemble within a single model. Similar to the ensemble, the final prediction is the aggregation of the prediction made by each learner. In contrast to previous works, our model can be trained end-to-end, alleviating the traditional cumbersome multi-stage training of ensembles. Our self-ensemble framework outperforms the current state-of-the-art on the benchmark datasets ADE20K, Pascal Context and COCO-Stuff-10K for semantic segmentation and is competitive on Cityscapes. Code will be available at github.com/WalBouss/SenFormer.

Adaptive Regularization of Ill-Posed Problems: Application to Non-rigid Image Registration

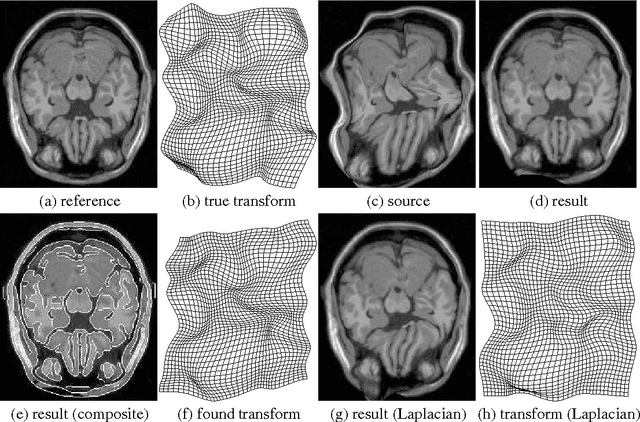
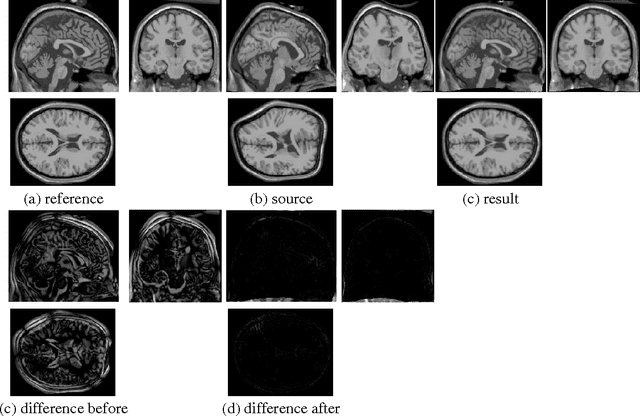
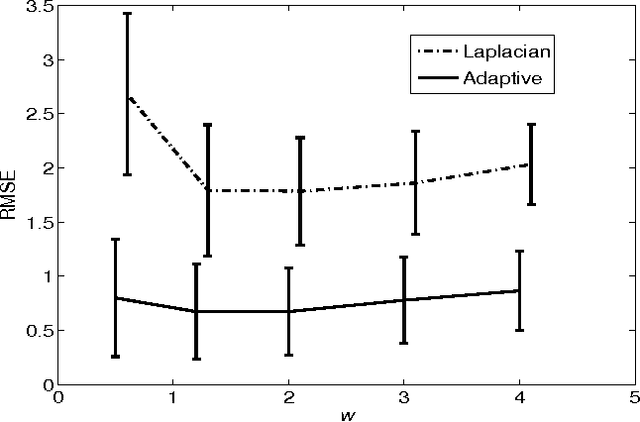
We introduce an adaptive regularization approach. In contrast to conventional Tikhonov regularization, which specifies a fixed regularization operator, we estimate it simultaneously with parameters. From a Bayesian perspective we estimate the prior distribution on parameters assuming that it is close to some given model distribution. We constrain the prior distribution to be a Gauss-Markov random field (GMRF), which allows us to solve for the prior distribution analytically and provides a fast optimization algorithm. We apply our approach to non-rigid image registration to estimate the spatial transformation between two images. Our evaluation shows that the adaptive regularization approach significantly outperforms standard variational methods.

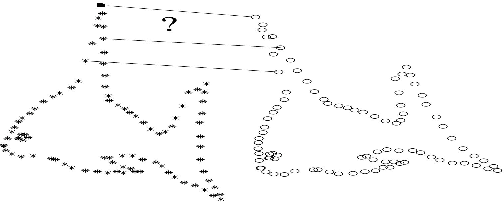
Point-Set Registration: Coherent Point Drift

Point set registration is a key component in many computer vision tasks. The goal of point set registration is to assign correspondences between two sets of points and to recover the transformation that maps one point set to the other. Multiple factors, including an unknown non-rigid spatial transformation, large dimensionality of point set, noise and outliers, make the point set registration a challenging problem. We introduce a probabilistic method, called the Coherent Point Drift (CPD) algorithm, for both rigid and non-rigid point set registration. We consider the alignment of two point sets as a probability density estimation problem. We fit the GMM centroids (representing the first point set) to the data (the second point set) by maximizing the likelihood. We force the GMM centroids to move coherently as a group to preserve the topological structure of the point sets. In the rigid case, we impose the coherence constraint by re-parametrization of GMM centroid locations with rigid parameters and derive a closed form solution of the maximization step of the EM algorithm in arbitrary dimensions. In the non-rigid case, we impose the coherence constraint by regularizing the displacement field and using the variational calculus to derive the optimal transformation. We also introduce a fast algorithm that reduces the method computation complexity to linear. We test the CPD algorithm for both rigid and non-rigid transformations in the presence of noise, outliers and missing points, where CPD shows accurate results and outperforms current state-of-the-art methods.

On the closed-form solution of the rotation matrix arising in computer vision problems

We show the closed-form solution to the maximization of trace(A'R), where A is given and R is unknown rotation matrix. This problem occurs in many computer vision tasks involving optimal rotation matrix estimation. The solution has been continuously reinvented in different fields as part of specific problems. We summarize the historical evolution of the problem and present the general proof of the solution. We contribute to the proof by considering the degenerate cases of A and discuss the uniqueness of R.