Disentangling Latent Risk Pathways via Bayesian Hypergraph Inference

Electronic health records (EHR) pose large-scale multi-disease modeling problems in which many outcomes are rare and strongly influenced by shared risk factors. While modern approaches achieve strong predictive performance, they often treat diseases independently or rely on black-box architectures, offering limited insight into how risk factors organize disease risk and little principled uncertainty quantification. We introduce a Bayesian hypergraph inference framework that reframes multi-disease modeling around latent, risk-factor-modulated disease pathways. Risk factors act on hyperedges, latent disease subsets with shared risk patterns, allowing diseases to participate in multiple distinct pathways and enabling interpretable, higher-order structure beyond pairwise associations. A repulsion prior encourages parsimonious and identifiable structure, while posterior inference provides calibrated uncertainty over both disease groupings and risk-factor influence. To enable scalable inference on large EHR datasets, we develop a structured variational inference algorithm that preserves logical dependencies among hyperedge existence, disease membership, and pathway-level effects. Experiments on simulated data and UK Biobank demonstrate stable and interpretable disease pathway structure, well-calibrated uncertainty, improved estimation for rare diseases, and competitive predictive performance.

Workflow Closure Is Not Scientific Closure in Auto-Research Systems

This paper argues that workflow closure is not scientific closure in auto-research systems. Current systems can increasingly complete research-like loops internally, moving from idea generation to experiment execution, writing, and self-evaluation. That achievement is real, but it does not by itself give the resulting outputs scientific standing. We argue that trustworthy auto-research should not aim for autonomous self-sufficiency, but should aim for autonomous execution under non-autonomous epistemic control. Based on a survey of more than 100 recent papers and repositories in this rapidly emerging area, together with a structured audit of 21 representative systems, we diagnose a recurring and structurally connected failure pattern: objective collapse, in which single-proxy targets replace multi-objective scientific aims; validation collapse, in which internal self-evaluation replaces independent validation; and acceptance collapse, in which benchmark scores or publication-shaped artifacts replace mechanisms for domain-level critique, reuse, and integration. These collapses are not inherent limits of autonomy but correctable design choices. Accordingly, we outline potential remedies across objective signal, validation, and output pathway to spark community discussion.

OnsagerNet: Learning Stable and Interpretable Dynamics using a Generalized Onsager Principle

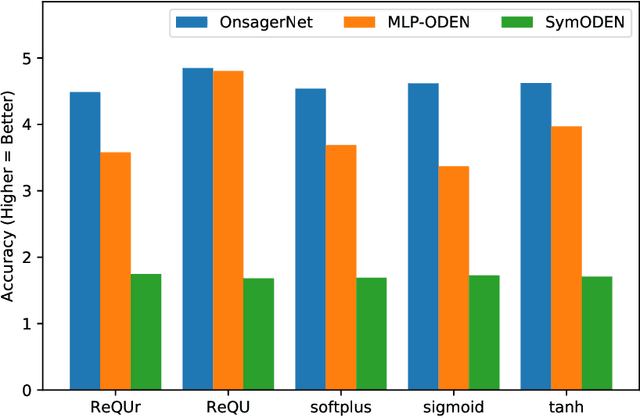
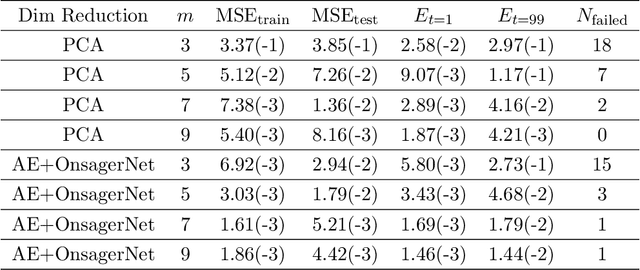
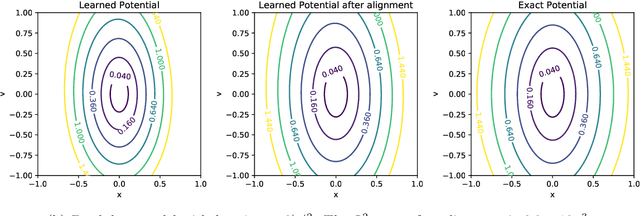
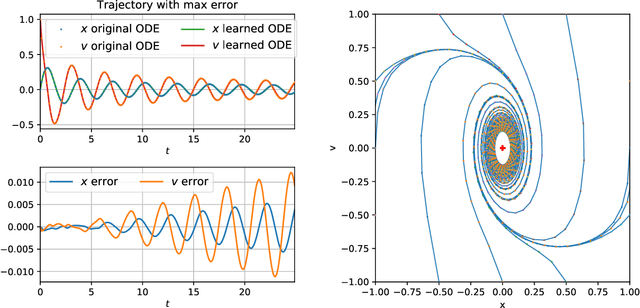
We propose a systematic method for learning stable and interpretable dynamical models using sampled trajectory data from physical processes based on a generalized Onsager principle. The learned dynamics are autonomous ordinary differential equations parameterized by neural networks that retain clear physical structure information, such as free energy, dissipation, conservative interaction and external force. The neural network representations for the hidden dynamics are trained by minimizing the empirical risk based on an embedded Runge-Kutta method. For high dimensional problems with a low dimensional slow manifold, an autoencoder with isometric regularization is introduced to find generalized coordinates on which we learn the Onsager dynamics. We apply the method to learn reduced order models for the Rayleigh-B\'{e}nard convection problem, where we obtain low dimensional autonomous equations that capture both qualitative and quantitative properties of the underlying dynamics. In particular, this validates the basic approach of Lorenz, although we also discover that the dimension of the learned autonomous model required for faithful representation increases with the Rayleigh number.