A Preliminary Comparison Between Compressive Sampling and Anisotropic Mesh-based Image Representation

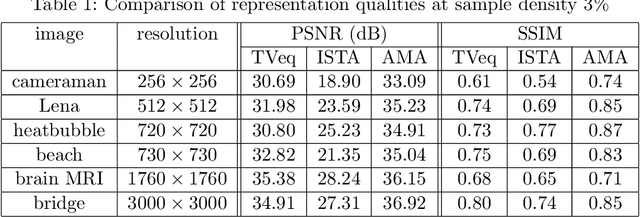
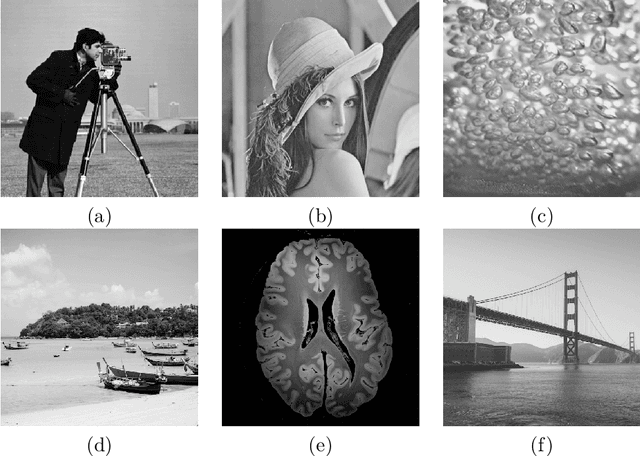
Compressed sensing (CS) has become a popular field in the last two decades to represent and reconstruct a sparse signal with much fewer samples than the signal itself. Although regular images are not sparse on their own, many can be sparsely represented in wavelet transform domain. Therefore, CS has also been widely applied to represent digital images. However, an alternative approach, adaptive sampling such as mesh-based image representation (MbIR), has not attracted as much attention. MbIR works directly on image pixels and represents the image with fewer points using a triangular mesh. In this paper, we perform a preliminary comparison between the CS and a recently developed MbIR method, AMA representation. The results demonstrate that, at the same sample density, AMA representation can provide better reconstruction quality than CS based on the tested algorithms. Further investigation with recent algorithms is needed to perform a thorough comparison.

Anisotropic Mesh Adaptation for Image Segmentation Based on Mumford-Shah Functional

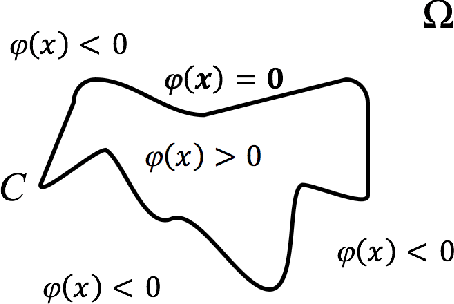
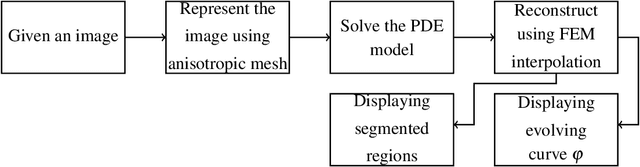
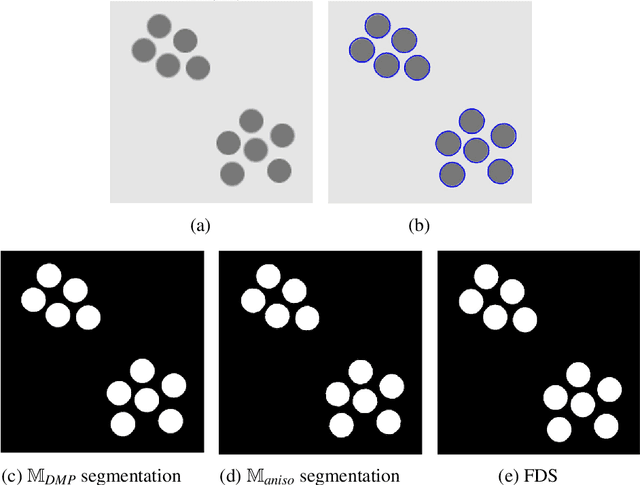
As the resolution of digital images increase significantly, the processing of images becomes more challenging in terms of accuracy and efficiency. In this paper, we consider image segmentation by solving a partial differentiation equation (PDE) model based on the Mumford-Shah functional. We develop a new algorithm by combining anisotropic mesh adaptation for image representation and finite element method for solving the PDE model. Comparing to traditional algorithms solved by finite difference method, our algorithm provides faster and better results without the need to resizing the images to lower quality. We also extend the algorithm to segment images with multiple regions.

Anisotropic Mesh Adaptation for Image Representation

Triangular meshes have gained much interest in image representation and have been widely used in image processing. This paper introduces a framework of anisotropic mesh adaptation (AMA) methods to image representation and proposes a GPRAMA method that is based on AMA and greedy-point removal (GPR) scheme. Different than many other methods that triangulate sample points to form the mesh, the AMA methods start directly with a triangular mesh and then adapt the mesh based on a user-defined metric tensor to represent the image. The AMA methods have clear mathematical framework and provides flexibility for both image representation and image reconstruction. A mesh patching technique is developed for the implementation of the GPRAMA method, which leads to an improved version of the popular GPRFS-ED method. The GPRAMA method can achieve better quality than the GPRFS-ED method but with lower computational cost.