Winfred Li
Universalizing Weak Supervision
Dec 07, 2021
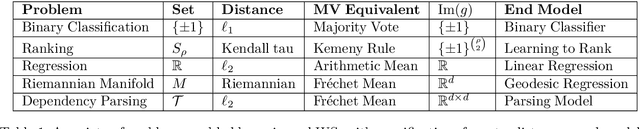
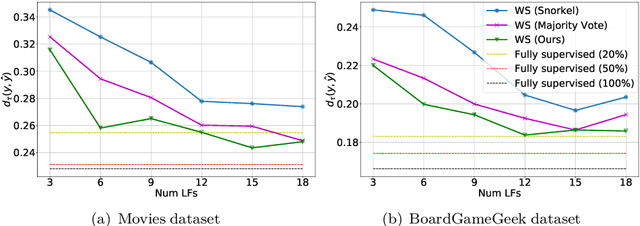
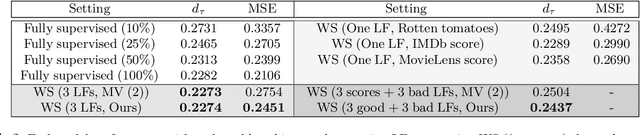
Abstract:Weak supervision (WS) frameworks are a popular way to bypass hand-labeling large datasets for training data-hungry models. These approaches synthesize multiple noisy but cheaply-acquired estimates of labels into a set of high-quality pseudolabels for downstream training. However, the synthesis technique is specific to a particular kind of label, such as binary labels or sequences, and each new label type requires manually designing a new synthesis algorithm. Instead, we propose a universal technique that enables weak supervision over any label type while still offering desirable properties, including practical flexibility, computational efficiency, and theoretical guarantees. We apply this technique to important problems previously not tackled by WS frameworks including learning to rank, regression, and learning in hyperbolic manifolds. Theoretically, our synthesis approach produces a consistent estimator for learning a challenging but important generalization of the exponential family model. Experimentally, we validate our framework and show improvement over baselines in diverse settings including real-world learning-to-rank and regression problems along with learning on hyperbolic manifolds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge