Generalized Information Bottleneck for Gaussian Variables

The information bottleneck (IB) method offers an attractive framework for understanding representation learning, however its applications are often limited by its computational intractability. Analytical characterization of the IB method is not only of practical interest, but it can also lead to new insights into learning phenomena. Here we consider a generalized IB problem, in which the mutual information in the original IB method is replaced by correlation measures based on Renyi and Jeffreys divergences. We derive an exact analytical IB solution for the case of Gaussian correlated variables. Our analysis reveals a series of structural transitions, similar to those previously observed in the original IB case. We find further that although solving the original, Renyi and Jeffreys IB problems yields different representations in general, the structural transitions occur at the same critical tradeoff parameters, and the Renyi and Jeffreys IB solutions perform well under the original IB objective. Our results suggest that formulating the IB method with alternative correlation measures could offer a strategy for obtaining an approximate solution to the original IB problem.

Information bottleneck theory of high-dimensional regression: relevancy, efficiency and optimality

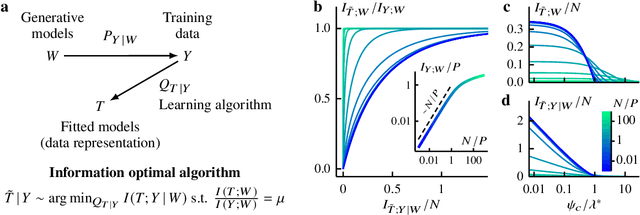
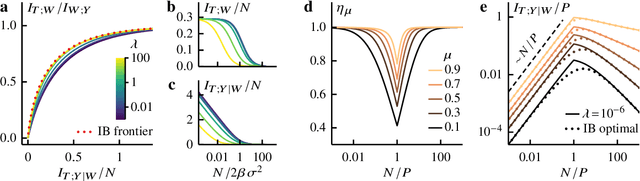
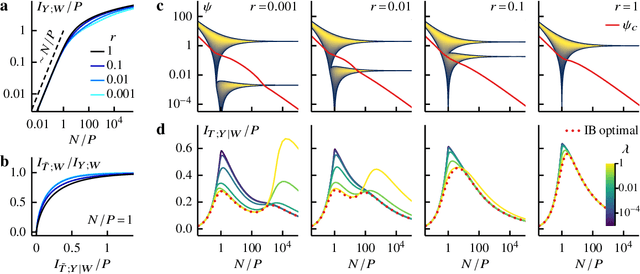
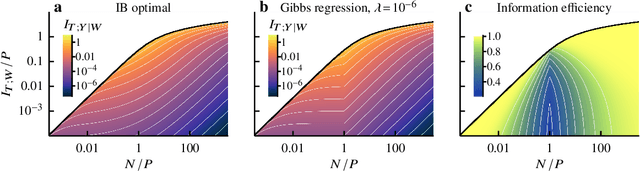
Avoiding overfitting is a central challenge in machine learning, yet many large neural networks readily achieve zero training loss. This puzzling contradiction necessitates new approaches to the study of overfitting. Here we quantify overfitting via residual information, defined as the bits in fitted models that encode noise in training data. Information efficient learning algorithms minimize residual information while maximizing the relevant bits, which are predictive of the unknown generative models. We solve this optimization to obtain the information content of optimal algorithms for a linear regression problem and compare it to that of randomized ridge regression. Our results demonstrate the fundamental tradeoff between residual and relevant information and characterize the relative information efficiency of randomized regression with respect to optimal algorithms. Finally, using results from random matrix theory, we reveal the information complexity of learning a linear map in high dimensions and unveil information-theoretic analogs of double and multiple descent phenomena.

Perturbation Theory for the Information Bottleneck

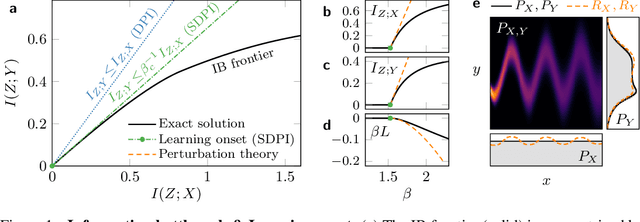
Extracting relevant information from data is crucial for all forms of learning. The information bottleneck (IB) method formalizes this, offering a mathematically precise and conceptually appealing framework for understanding learning phenomena. However the nonlinearity of the IB problem makes it computationally expensive and analytically intractable in general. Here we derive a perturbation theory for the IB method and report the first complete characterization of the learning onset, the limit of maximum relevant information per bit extracted from data. We test our results on synthetic probability distributions, finding good agreement with the exact numerical solution near the onset of learning. We explore the difference and subtleties in our derivation and previous attempts at deriving a perturbation theory for the learning onset and attribute the discrepancy to a flawed assumption. Our work also provides a fresh perspective on the intimate relationship between the IB method and the strong data processing inequality.