Pseudo-Observations and Super Learner for the Estimation of the Restricted Mean Survival Time

In the context of right-censored data, we study the problem of predicting the restricted time to event based on a set of covariates. Under a quadratic loss, this problem is equivalent to estimating the conditional Restricted Mean Survival Time (RMST). To that aim, we propose a flexible and easy-to-use ensemble algorithm that combines pseudo-observations and super learner. The classical theoretical results of the super learner are extended to right-censored data, using a new definition of pseudo-observations, the so-called split pseudo-observations. Simulation studies indicate that the split pseudo-observations and the standard pseudo-observations are similar even for small sample sizes. The method is applied to maintenance and colon cancer datasets, showing the interest of the method in practice, as compared to other prediction methods. We complement the predictions obtained from our method with our RMST-adapted risk measure, prediction intervals and variable importance measures developed in a previous work.

Error rate control for classification rules in multiclass mixture models

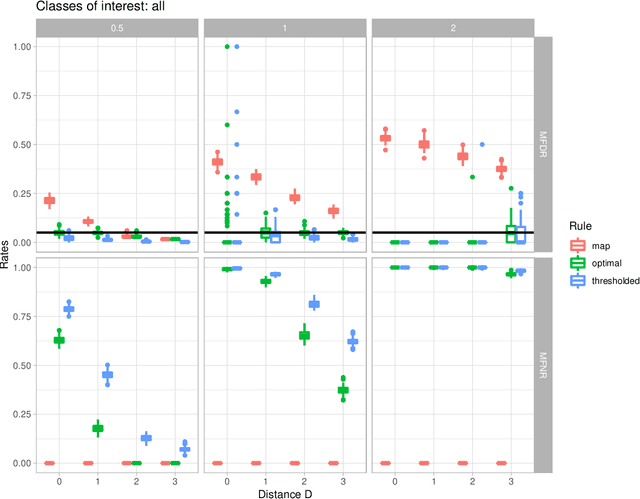
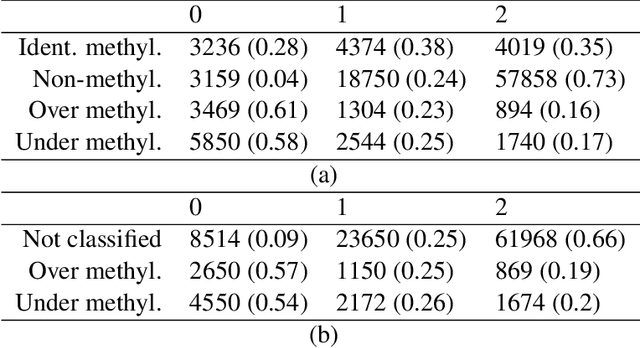
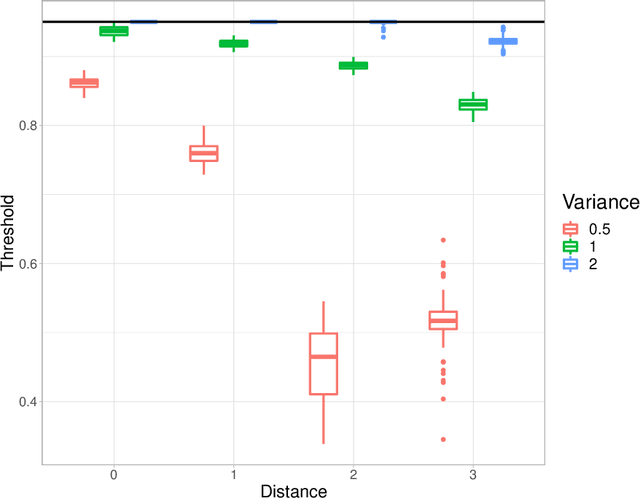
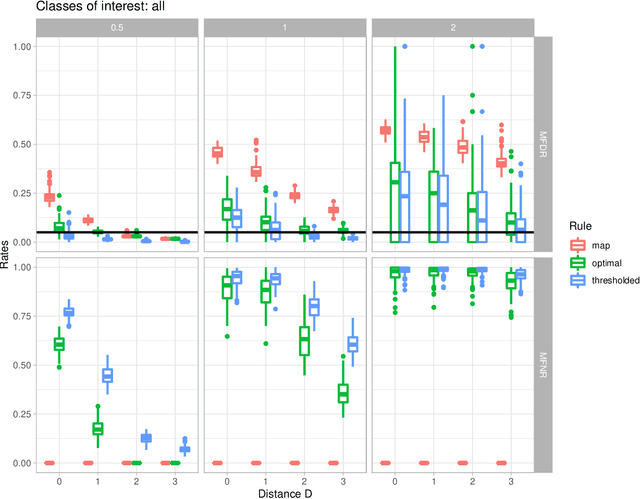
In the context of finite mixture models one considers the problem of classifying as many observations as possible in the classes of interest while controlling the classification error rate in these same classes. Similar to what is done in the framework of statistical test theory, different type I and type II-like classification error rates can be defined, along with their associated optimal rules, where optimality is defined as minimizing type II error rate while controlling type I error rate at some nominal level. It is first shown that finding an optimal classification rule boils down to searching an optimal region in the observation space where to apply the classical Maximum A Posteriori (MAP) rule. Depending on the misclassification rate to be controlled, the shape of the optimal region is provided, along with a heuristic to compute the optimal classification rule in practice. In particular, a multiclass FDR-like optimal rule is defined and compared to the thresholded MAP rules that is used in most applications. It is shown on both simulated and real datasets that the FDR-like optimal rule may be significantly less conservative than the thresholded MAP rule.

Measuring the Influence of Observations in HMMs through the Kullback-Leibler Distance

We measure the influence of individual observations on the sequence of the hidden states of the Hidden Markov Model (HMM) by means of the Kullback-Leibler distance (KLD). Namely, we consider the KLD between the conditional distribution of the hidden states' chain given the complete sequence of observations and the conditional distribution of the hidden chain given all the observations but the one under consideration. We introduce a linear complexity algorithm for computing the influence of all the observations. As an illustration, we investigate the application of our algorithm to the problem of detecting outliers in HMM data series.