Realistic Image-to-Image Machine Unlearning via Decoupling and Knowledge Retention

Machine Unlearning allows participants to remove their data from a trained machine learning model in order to preserve their privacy, and security. However, the machine unlearning literature for generative models is rather limited. The literature for image-to-image generative model (I2I model) considers minimizing the distance between Gaussian noise and the output of I2I model for forget samples as machine unlearning. However, we argue that the machine learning model performs fairly well on unseen data i.e., a retrained model will be able to catch generic patterns in the data and hence will not generate an output which is equivalent to Gaussian noise. In this paper, we consider that the model after unlearning should treat forget samples as out-of-distribution (OOD) data, i.e., the unlearned model should no longer recognize or encode the specific patterns found in the forget samples. To achieve this, we propose a framework which decouples the model parameters with gradient ascent, ensuring that forget samples are OOD for unlearned model with theoretical guarantee. We also provide $(\epsilon, \delta)$-unlearning guarantee for model updates with gradient ascent. The unlearned model is further fine-tuned on the remaining samples to maintain its performance. We also propose an attack model to ensure that the unlearned model has effectively removed the influence of forget samples. Extensive empirical evaluation on two large-scale datasets, ImageNet-1K and Places365 highlights the superiority of our approach. To show comparable performance with retrained model, we also show the comparison of a simple AutoEncoder on various baselines on CIFAR-10 dataset.

Unlearning Clients, Features and Samples in Vertical Federated Learning

Federated Learning (FL) has emerged as a prominent distributed learning paradigm. Within the scope of privacy preservation, information privacy regulations such as GDPR entitle users to request the removal (or unlearning) of their contribution from a service that is hosting the model. For this purpose, a server hosting an ML model must be able to unlearn certain information in cases such as copyright infringement or security issues that can make the model vulnerable or impact the performance of a service based on that model. While most unlearning approaches in FL focus on Horizontal FL (HFL), where clients share the feature space and the global model, Vertical FL (VFL) has received less attention from the research community. VFL involves clients (passive parties) sharing the sample space among them while not having access to the labels. In this paper, we explore unlearning in VFL from three perspectives: unlearning clients, unlearning features, and unlearning samples. To unlearn clients and features we introduce VFU-KD which is based on knowledge distillation (KD) while to unlearn samples, VFU-GA is introduced which is based on gradient ascent. To provide evidence of approximate unlearning, we utilize Membership Inference Attack (MIA) to audit the effectiveness of our unlearning approach. Our experiments across six tabular datasets and two image datasets demonstrate that VFU-KD and VFU-GA achieve performance comparable to or better than both retraining from scratch and the benchmark R2S method in many cases, with improvements of $(0-2\%)$. In the remaining cases, utility scores remain comparable, with a modest utility loss ranging from $1-5\%$. Unlike existing methods, VFU-KD and VFU-GA require no communication between active and passive parties during unlearning. However, they do require the active party to store the previously communicated embeddings.

Efficient Federated Unlearning under Plausible Deniability

Privacy regulations like the GDPR in Europe and the CCPA in the US allow users the right to remove their data ML applications. Machine unlearning addresses this by modifying the ML parameters in order to forget the influence of a specific data point on its weights. Recent literature has highlighted that the contribution from data point(s) can be forged with some other data points in the dataset with probability close to one. This allows a server to falsely claim unlearning without actually modifying the model's parameters. However, in distributed paradigms such as FL, where the server lacks access to the dataset and the number of clients are limited, claiming unlearning in such cases becomes a challenge. This paper introduces an efficient way to achieve federated unlearning, by employing a privacy model which allows the FL server to plausibly deny the client's participation in the training up to a certain extent. We demonstrate that the server can generate a Proof-of-Deniability, where each aggregated update can be associated with at least x number of client updates. This enables the server to plausibly deny a client's participation. However, in the event of frequent unlearning requests, the server is required to adopt an unlearning strategy and, accordingly, update its model parameters. We also perturb the client updates in a cluster in order to avoid inference from an honest but curious server. We show that the global model satisfies differential privacy after T number of communication rounds. The proposed methodology has been evaluated on multiple datasets in different privacy settings. The experimental results show that our framework achieves comparable utility while providing a significant reduction in terms of memory (30 times), as well as retraining time (1.6-500769 times). The source code for the paper is available.

The transport problem for non-additive measures

Non-additive measures, also known as fuzzy measures, capacities, and monotonic games, are increasingly used in different fields. Applications have been built within computer science and artificial intelligence related to e.g. decision making, image processing, machine learning for both classification, and regression. Tools for measure identification have been built. In short, as non-additive measures are more general than additive ones (i.e., than probabilities), they have better modeling capabilities allowing to model situations and problems that cannot be modeled by the latter. See e.g. the application of non-additive measures and the Choquet integral to model both Ellsberg paradox and Allais paradox. Because of that, there is an increasing need to analyze non-additive measures. The need for distances and similarities to compare them is no exception. Some work has been done for defining $f$-divergence for them. In this work we tackle the problem of defining the optimal transport problem for non-additive measures. Distances for pairs of probability distributions based on the optimal transport are extremely used in practical applications, and they are being studied extensively for their mathematical properties. We consider that it is necessary to provide appropriate definitions with a similar flavour, and that generalize the standard ones, for non-additive measures. We provide definitions based on the M\"obius transform, but also based on the $(\max, +)$-transform that we consider that has some advantages. We will discuss in this paper the problems that arise to define the transport problem for non-additive measures, and discuss ways to solve them. In this paper we provide the definitions of the optimal transport problem, and prove some properties.

Literature Review of various Fuzzy Rule based Systems

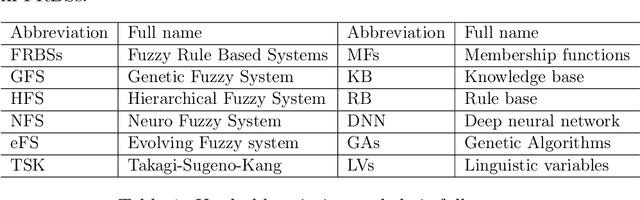
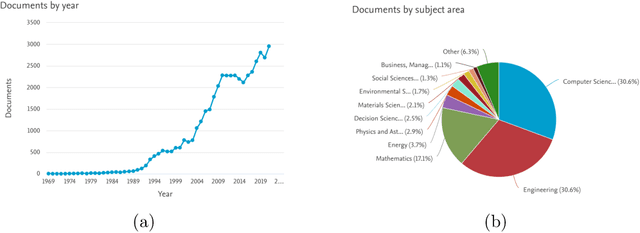
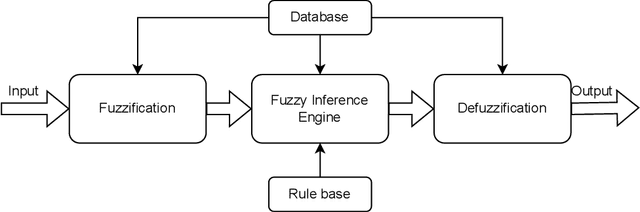
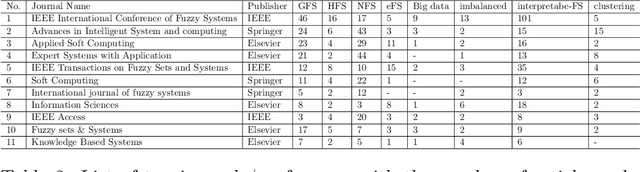
Fuzzy rule based systems (FRBSs) is a rule-based system which uses linguistic fuzzy variables as antecedents and consequent to represent the human understandable knowledge. They have been applied to various applications and areas throughout the literature. However, FRBSs suffers from many drawbacks such as uncertainty representation, high number of rules, interpretability loss, high computational time for learning etc. To overcome these issues with FRBSs, there exists many extentions of FRBSs. In this paper, we present an overview and literature review for various types and prominent areas of fuzzy systems (FRBSs) namely genetic fuzzy system (GFS), Hierarchical fuzzy system (HFS), neuro fuzzy system (NFS), evolving fuzzy system (eFS), FRBSs for big data, FRBSs for imbalanced data, interpretability in FRBSs and FRBSs which uses cluster centroids as fuzzy rule, during the years 2010-2021. GFS uses genetic/evolutionary approaches to improve the learning ability of FRBSs, HFS solve the curse of dimensionality for FRBSs, NFS improves approximation ability of FRBSs using neural networks and dynamic systems for streaming data is considered in eFS. FRBSs are seen as good solutions for big data and imbalanced data, in the recent years the interpretability in FRBSs has gained popularity due to high dimensional and big data and rules are initialized with cluster centroids to limit the number of rules in FRBSs. This paper also highlights important contributions, publication statistics and current trends in the field. The paper also addresses several open research areas which need further attention from the FRBSs research community.

A formalization of re-identification in terms of compatible probabilities

Re-identification algorithms are used in data privacy to measure disclosure risk. They model the situation in which an adversary attacks a published database by means of linking the information of this adversary with the database. In this paper we formalize this type of algorithm in terms of true probabilities and compatible belief functions. The purpose of this work is to leave aside as re-identification algorithms those algorithms that do not satisfy a minimum requirement.